
题目列表(包括答案和解析)
(本大题满分14分)
已知数列 和
和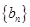 满足:
满足: ,
, ,
,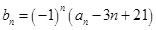 ,其中
,其中 为实数,
为实数, 为正整数.
为正整数.
(Ⅰ)对任意实数 ,证明:数列
,证明:数列 不是等比数列;
不是等比数列;
(Ⅱ)证明:当 时,数列
时,数列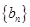 是等比数列;
是等比数列;
(Ⅲ)设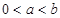 (
( 为实常数),
为实常数),  为数列
为数列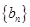 的前
的前 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本大题满分14分)
设函数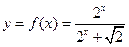 上两点
上两点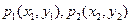 ,若
,若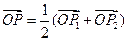 ,且P点的横坐标为
,且P点的横坐标为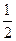 .
.
(1)求P点的纵坐 标;
标;
(2)若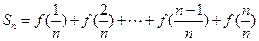 求
求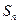 ;
;
(3)记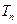 为数列
为数列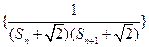 的前n项和,若
的前n项和,若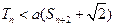 对一切
对一切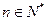 都成立,试求a的取值范围.
都成立,试求a的取值范围.
(本大题满分14分)
已知数列{an}的前n项和Sn是二项式![]() 展开式中含x奇次幂的系数和.
展开式中含x奇次幂的系数和.
(1)求数列{an}的通项公式;
(2)设![]() ,求
,求![]() ;
;
(3)证明:![]() .
.
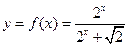 上两点
上两点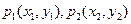 ,若
,若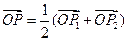 ,且P点的横坐标为
,且P点的横坐标为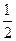 .
. 标;
标;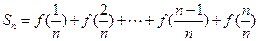 求
求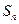 ;
;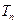 为数列
为数列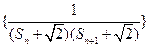 的前n项和,若
的前n项和,若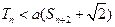 对一切
对一切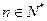 都成立,试求a的取值范围.
都成立,试求a的取值范围. (本大题满分14分)
已知关于x的不等式![]() 的解集为A,且
的解集为A,且![]()
(1)求实数![]() 的取值范围;
的取值范围;
(2)并用![]() 表示出该不等式的解集A.
表示出该不等式的解集A.
说明:
一、本解答指出了每题要考察的主要知识和能力,并给出了一种或几种解法供参考,如
果考生的解法与本解法不同,可根据试题的主要考察内容比照评分标准指定相应的评分细
则。
二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程
度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答
有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分。
一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分。
1.B 2.A 3.B 4.A 5.B 6.C 7.A 8.B 9.C 10.B 11.D 12.D
二、填空题:本题考查基础知识和基本运算,每小题4分,满分16分。
13.1 14. 15.5 16.8
15.5 16.8
三、解答题:本大题共6小题,满分74分,解答须写出文字说明、证明过程和演算步骤。
17.本题主要考查平面向量的数量积,两角和与差的三角函数公式、二倍角公式,三角函数的图象与性质等基础知识;考查运算求解能力,满分12分。
解:
(I)
 ………………………………………2分
………………………………………2分
即函数 的解析式为
的解析式为 ?????????????????????????????????????? 4分
?????????????????????????????????????? 4分
(Ⅱ) ??????????????????????????????????????? 6分
??????????????????????????????????????? 6分
所以函数 最小正周期
最小正周期 ???????????????????????????????????????????????????? 8分
???????????????????????????????????????????????????? 8分
当 即
即 时
时
 取最大值
取最大值 ,?????????????????????????????????????????????????????????????????????????? 10分
,?????????????????????????????????????????????????????????????????????????? 10分
 使函数取最大值的
使函数取最大值的 的集合为
的集合为 ???????????????????????????????? 12分
???????????????????????????????? 12分
18.本题主要考查空间几何体的直观图、三视图,空间线面的位置关系等基础知识;考察空间想象能力及推理论证能力,满分12分。
解(I)由三视图知这个多面体是一个水平放置的柱体,它的底面是边长为 的正三角形,侧棱垂直于底面且长为
的正三角形,侧棱垂直于底面且长为 2分
2分
 ??????????????????????????????????????????????????????????????????????????????? 3分
??????????????????????????????????????????????????????????????????????????????? 3分
 ???????????????????????????????????????????????????????????????????? 5分
???????????????????????????????????????????????????????????????????? 5分
(Ⅱ)连结
 四边形
四边形 是平行四边形,
是平行四边形,


 过点
过点 。
。

 为
为 的中点,………………………………………8分
的中点,………………………………………8分
又 是
是 的中点,
的中点,
 ,
,
 平面
平面 平面
平面
 平面
平面 …………………………………………12分
…………………………………………12分
19.本题主要考等差数列、数列求和等基础知识:考查推理论证与运算求解能力;考查化归与转化思想,满分12分。
解(I) 点
点 在函数
在函数 的图象上,
的图象上,

 数列
数列 是以首项为2公差为2的等差数列,???????????????????????????????????????? 2分
是以首项为2公差为2的等差数列,???????????????????????????????????????? 2分
 ?????????????????????????????????????????????????????????????????????? 4分
?????????????????????????????????????????????????????????????????????? 4分
(Ⅱ) ????????????????????????????????????????????????????????????? 6分
????????????????????????????????????????????????????????????? 6分
 ,????????????????????????????????????????????????????????????????? 8分
,????????????????????????????????????????????????????????????????? 8分
 ???????????????????????? 10分
???????????????????????? 10分
 ?????????????????????????????????????????????????????????????????????????????? 12分
?????????????????????????????????????????????????????????????????????????????? 12分
20.本题主要考查概率与统计的基础知识,考查运算求解能力及应用意识。
满分12分。
解:(I)设样本容量为 ,则
,则 ,所以
,所以
所以样本的容量为120???????????????????????????????????????????????????????????????????????? 3分
(Ⅱ)设成绩在120分到150分的学生有 个,
个,
则 ,所以
,所以 ????????????????????????????????????????????????????????????????????? 3分
????????????????????????????????????????????????????????????????????? 3分
(Ⅲ)设成绩在120分到150分的学生中,男生比女生多的事件记为A,男生数与女生书记为数对( ),则基本事件有:(5,15),(6,14),(7,13),(8,12),(9,11),
),则基本事件有:(5,15),(6,14),(7,13),(8,12),(9,11),
(10,10),(11,9),(12,8),(13,7),(14,6),(15,5),(16,4),(17,3),
(18,2),(19,1),(20,0),共16对????????????????????????????????????????????????? 9分
而事件A包含的事件有:(11,9),(12,8),(13,7),(14,6),(15,5),(16,4),
(17,3),(18,2),(19,1),(20,0)共10对。
所以 ??????????????????????????????????????????????????????????????????????????? 12分
??????????????????????????????????????????????????????????????????????????? 12分
21.本题主要考查利用导数研究函数的性质,考查运算求解能力及数形结合思想。满分12分。
解:(I)
 ????????????????????????????????????????????????????????????????????????????????? 2分
????????????????????????????????????????????????????????????????????????????????? 2分
依题意得 ??????????????????????????????????????????????????????????????????? 4分
??????????????????????????????????????????????????????????????????? 4分
(Ⅱ)
 等价于
等价于 ???????????????????????????????????????????????????? 6分
???????????????????????????????????????????????????? 6分
①当 时
时 恒成立,
恒成立,
 的单调递增区间为
的单调递增区间为 ?????????????????????????????????????????????????????????? 8分
?????????????????????????????????????????????????????????? 8分
②当 时,由
时,由 得
得

 的单调递增区间为
的单调递增区间为 ?????????????????????????????????????????????????????? 11分
?????????????????????????????????????????????????????? 11分
综上所述:当 时
时 的单调递增区间为
的单调递增区间为 ;
;
当 时,
时, 的单调递增区间为
的单调递增区间为 ???????????????????????????????????????? 12分
???????????????????????????????????????? 12分
22.本题主要考查直线与椭圆的位置关系等基础知识;考查运算求解能力及化归与转化思想。满分14分。
解:(I)设椭圆E的方程为
由已知得:
 ??????????????????????????????????????????????????????????????????????????????????????? 2分
??????????????????????????????????????????????????????????????????????????????????????? 2分


 椭圆E的方程为
椭圆E的方程为 ?????????????????????????????????????????????????????????????? 4分
?????????????????????????????????????????????????????????????? 4分
 (Ⅱ)设
(Ⅱ)设 ,线段
,线段 中点
中点 的坐标为
的坐标为 ,则:
,则:
由 得
得
化简得:
 ……5分
……5分
 直线
直线 过点
过点
而点 在椭圆E内,
在椭圆E内,
 ?????????????????????????????????????????????????????????? 6分
?????????????????????????????????????????????????????????? 6分

所以PQ中垂直 的方程为:
的方程为:
所以直线 在
在 轴上的截距
轴上的截距 ??????????????????????????????????????? 8分
??????????????????????????????????????? 8分
 ??????????????????????????????????????????????????????????? 9分
??????????????????????????????????????????????????????????? 9分
(Ⅲ)假设存在符号条件的点 ,则由(Ⅱ)得:
,则由(Ⅱ)得:

 ????????????????????????????????????????????????? 10分
????????????????????????????????????????????????? 10分

 ????????????????????????? 11分
????????????????????????? 11分
所以
 ?????????????????????????????????????????? 12分
?????????????????????????????????????????? 12分
设
即

对于任意实数 ,上式恒成立,
,上式恒成立,
所以 ????????????????????????????????????????????????????????????????????? 13分
????????????????????????????????????????????????????????????????????? 13分
得
所以符合条件的点 存在,其坐标为
存在,其坐标为 ???????????????????????????????????????????? 14分
???????????????????????????????????????????? 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com