
题目列表(包括答案和解析)
 (本小题满分12分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(本小题满分12分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(I)设![]() (单位:米),要使花坛AMPN的面积大于32平方米,求
(单位:米),要使花坛AMPN的面积大于32平方米,求![]() 的取值范围;
的取值范围;
(II)若![]() (单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(本小题满分12分)
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上,  点在
点在 上,且对角线
上,且对角线 过点
过点 ,已知
,已知 米,
米, 米.
米.
(1)要使矩形 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(2)当 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值.
(本小题满分12分)
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上,  点在
点在 上,且对角线
上,且对角线 过点
过点 ,已知
,已知 米,
米,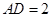 米.
米.
(1)要使矩形 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(2)当 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值.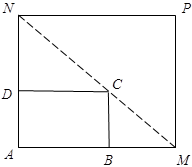
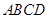 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛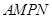 ,要求
,要求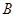 点在
点在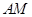 上,
上, 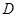 点在
点在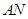 上,且对角线
上,且对角线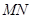 过点
过点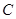 ,已知
,已知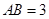 米,
米,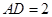 米.
米.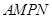 的面积大于32平方米,则
的面积大于32平方米,则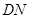 的长应在什么范围内?
的长应在什么范围内?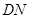 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛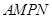 的面积最小?并求出最小值.
的面积最小?并求出最小值.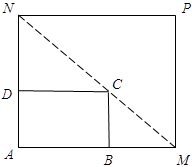
(本小题满分12分)
如图所示,将一矩形花坛![]() 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛![]() ,要求B点在
,要求B点在![]() 上,
上,![]() 点在
点在![]() 上,且对角戏
上,且对角戏![]() 过
过![]() 点,已知
点,已知![]() =3米,
=3米,![]() =2米.
=2米.
(1)要使矩形![]() 的面积大于32平方米,则
的面积大于32平方米,则![]() 的长应在什么范围内?
的长应在什么范围内?
(2)当![]() 的长为多少时,矩形花坛
的长为多少时,矩形花坛![]() 的面积最小?并求出最小值.
的面积最小?并求出最小值.
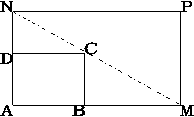 |
一、选择题
1.D 2.B 3.C 4.D 5.B 6.C 7.C 8.D 9.C 10.D
二、填空题
11. 12.
12. 13.
13. 14.2+
14.2+ 15.
15.
三、解答题
16.⑴∵ 1分
1分
= 3分
3分
又由 得
得 ∴
∴ 5分
5分
故 ,f (x)max=1+2×1=3 6分
,f (x)max=1+2×1=3 6分
⑵ <2在
<2在 上恒成立
上恒成立
 时
时 9分
9分
结合⑴知: 故m的取值范围是(1,4) 12分
故m的取值范围是(1,4) 12分
17.⑴连结AC,△ABC为正△,又E为BC中点,∴AE⊥BC又AD∥BC
∴AE⊥AD,又PA⊥平面ABCD
故AD为PD在平面ABCD内的射影,由三垂线定理知:AE⊥PD。 4分
⑵连HA,由EA⊥平面PAD知∠AHE为EH与平面PAD所成线面角 5分
而tan∠AHE= 故当AH最小即AH⊥PD时EH与平面PAD所成角最大
故当AH最小即AH⊥PD时EH与平面PAD所成角最大
6分
令AB=2,则AE= ,此时
,此时
∴AH= ,由平几知识得PA=2 7分
,由平几知识得PA=2 7分
因为PA⊥平面ABCD,PA 平面PAC,所以平面PAC⊥平面ABCD
平面PAC,所以平面PAC⊥平面ABCD
过E作EO⊥AC于O,则EO⊥平面PAC
过O作OS⊥AF于S,连结ES,则∠ESO
为二面角E―AF―C的平面角 9分
在Rt△AOE中,EO=AE?sin30o= ,AO=AE?cos30o=
,AO=AE?cos30o=
又F是PC的中点,在Rt△ASO中,SO=AO?sin45o=
又SE= ,在Rt△ESO中,cos∠ESO=
,在Rt△ESO中,cos∠ESO=
即所求二面角的余弦值为 12分
12分
注:向量法及其它方法可参照给分。
18.⑴设平均数为 ,
,
即测量50次的平均值为
⑵ 7分
7分
⑶每一次测得数据为 10分
10分
故所求概率 12分
12分
19.⑴容器底面是边长为(2-2x)的正三角形,高为x
∴ ∴
∴
故定义域为
⑵ ,
, 5分
5分
令V'=0得x< 或x>1;V'<0得
或x>1;V'<0得
∴V在(0, )和(1,+∞)上单调递增,在(
)和(1,+∞)上单调递增,在( ,1)上单调递减
,1)上单调递减
当 时,x=
时,x= 时,V最大,Vmax=V(
时,V最大,Vmax=V( )=
)=
当 即
即 时,由V在(0,
时,由V在(0, )上递增知
)上递增知
x= 时,V最大,Vmax=
时,V最大,Vmax=
20.⑴由 得ax2+(
得ax2+(
∴当且仅当 时,
时, 有唯一解x=0,∴
有唯一解x=0,∴
当 得x1=2,由
得x1=2,由
∴数列 是首项为
是首项为 ,公差为
,公差为 的等差数列
的等差数列
∴ 7分
7分
⑵ 又
又
∴ 且an>0,a2=
且an>0,a2=
∴
即
当n≥2时,


故
21.⑴设椭圆方程为 ,F(c,0)
,F(c,0)
则AB∶y=x-c代入 得(a2+b2)x2-
得(a2+b2)x2-
令A(x1、y1)、B(x2、y2),则
由 与
与 共线
共线
得3(y1+y2)+(x1+x2)=0,又y1=x1-c,y2=x2-c
∴3(x1+x2-
∴ 即a2=3b2,故
即a2=3b2,故 7分
7分
⑵由⑴知a2=3b2,椭圆方程 可化为x2+3y2=3b2
可化为x2+3y2=3b2
设 =(x,y),则(x,y)=λ(x1,y1)+μ(x2,y2)
=(x,y),则(x,y)=λ(x1,y1)+μ(x2,y2)
∴
∵M(x,y)在椭圆上
∴(λx1+μx2)2+(λy2+μy2)2=3b2
即λ2(x12+3y12)+μ2(3x22+3y22)+2λμ(x1x2+3y1y2)=3b2 ①
由⑴知,x1+x2= ,a2=
,a2= ,b2=
,b2=
∴x1x2=
∴x1x2+3y1y2=x1x2+3(x1-c)(x2-c)=4x1x2-3(x1+x2)c+
=
又x12+3y12=3b2,x22+3y22=3b2代入①得λ2+μ2=1 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com