
题目列表(包括答案和解析)
| 1 |
| bn |
| 1-m |
| 1005 |
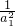 +
+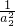 +…+
+…+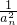 <
< .
.| 1 |
| bn |
| 1-m |
| 1005 |
一.选择题
序号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
D
C
A
C
C
B
D
A
二填空题
13.卷.files/image191.gif) ; 14.-6 ; 15.
; 14.-6 ; 15.卷.files/image193.gif) ; 16.
; 16.卷.files/image064.gif) .
.
三.解答题
17.解:(Ⅰ)卷.files/image196.gif)
卷.files/image198.gif) ………………………………………………………………4分
………………………………………………………………4分
卷.files/image200.gif) …………………………6分
…………………………6分
(Ⅱ)卷.files/image202.gif) …………………………………………………8分
…………………………………………………8分
卷.files/image204.gif)
∴卷.files/image206.gif) …………………………………………………………………………10分
…………………………………………………………………………10分
卷.files/image208.gif) ………………………………………………………………………………12分
………………………………………………………………………………12分
18.解:(Ⅰ)在Rt△ABC中,AB=1,∠BAC=60°,∴BC=卷.files/image210.gif) ,AC=2.
,AC=2.
在Rt△ACD中,AC=2,∠CAD=60°,∴CD=2卷.files/image210.gif) ,AD=4.
,AD=4.
∴卷.files/image212.gif) =
=卷.files/image214.gif)
卷.files/image216.gif) .……………………………………………………………… 2分
.……………………………………………………………… 2分
则V=卷.files/image218.gif) . ……………………………………………………………… 4分
. ……………………………………………………………… 4分
(Ⅱ)∵PA=CA,F为PC的中点,∴AF⊥PC. …………………………5分
∵PA⊥平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.∴CD⊥PC.
∵E为PD中点,F为PC中点,∴EF∥CD.则EF⊥PC. …………………………7分
∵AF∩EF=F,∴PC⊥平面AEF.…………………………………………………………8分
(Ⅲ)以A为坐标原点,AD,AP所在直线分别为y轴,z轴,建立空间直角坐标系,
则平面PAD的法向量为:卷.files/image220.gif) =(1,0,0)
=(1,0,0)
由(Ⅱ)知AF⊥PC,AF⊥CD ∴AF⊥平面PCD
∴卷.files/image222.gif) 为平面PCD的法向量.
为平面PCD的法向量.
∵P(0,0,2),C卷.files/image224.gif) ∴
∴卷.files/image222.gif) =
=卷.files/image227.gif)
卷.files/image229.gif) ,即二面角C-PD-A的余弦值为
,即二面角C-PD-A的余弦值为卷.files/image231.gif) …………12分
…………12分
19.解:设第一个匣子里的三把钥匙为A,B,C,第二个匣子里的三把钥匙为a,b,c(设A,a能打开所有门,B只能打开第一道门,b只能打开第二道门,C,c不能打开任何一道门)
(Ⅰ)卷.files/image233.gif) …………………………………………………………………………4分
…………………………………………………………………………4分
(Ⅱ)卷.files/image235.gif) (第一次只能拿B,第二次只能拿c) ……………………………6分
(第一次只能拿B,第二次只能拿c) ……………………………6分
卷.files/image237.gif) (第一次只能拿B,第二次只能拿b)
……………………………8分
(第一次只能拿B,第二次只能拿b)
……………………………8分
卷.files/image239.gif) (第一次拿A,第二次随便拿,或第一次拿B,第二次拿a) …10分
(第一次拿A,第二次随便拿,或第一次拿B,第二次拿a) …10分
卷.files/image241.gif) …………………………12分
…………………………12分
20.(Ⅰ)依题卷.files/image243.gif)
卷.files/image245.gif)
卷.files/image247.gif)
卷.files/image249.gif)
即卷.files/image251.gif)
卷.files/image253.gif) (
(卷.files/image255.gif) …………………………………………………3分
…………………………………………………3分
故卷.files/image147.gif) 为等差数列,a1=1,d=2
为等差数列,a1=1,d=2
卷.files/image258.gif) ………………………………………………………………………………………………5分
………………………………………………………………………………………………5分
(Ⅱ)设公比为q,则由b1b2b3=8,bn>0卷.files/image260.gif) …………………………………………………6分
…………………………………………………6分
又卷.files/image262.gif) 成等差数列
成等差数列
卷.files/image264.gif) ………………………………………………………………………………………8分
………………………………………………………………………………………8分
卷.files/image266.gif) 或
或卷.files/image268.gif) …………………………………………………………………………………10分
…………………………………………………………………………………10分
卷.files/image270.gif) 或
或卷.files/image272.gif) ……………………………………………………………………12分
……………………………………………………………………12分
21解:(Ⅰ)依题PN为AM的中垂线
卷.files/image274.gif)
卷.files/image276.gif) …………………………………………………………2分
…………………………………………………………2分
又C(-1,0),A(1,0)
所以N的轨迹E为椭圆,C、A为其焦点…………………………………………………………4分
a=卷.files/image064.gif) ,c=1,所以
,c=1,所以卷.files/image279.gif) 为所求………………………………………………………5分
为所求………………………………………………………5分
(Ⅱ)设直线卷.files/image098.gif) 的方程为:y=k(x-1)代入椭圆方程:x2+2y2=2得
的方程为:y=k(x-1)代入椭圆方程:x2+2y2=2得
(1+2k2)x2-4k2x+2k2-2=0………………(1)
设G(x1,y1)、H(x2,y2),则x1,x2是(1)的两个根.
卷.files/image281.gif) …………………………………………………………7分
…………………………………………………………7分
依题卷.files/image283.gif)
卷.files/image285.gif)
卷.files/image287.gif)
卷.files/image289.gif) ………………………………………………………9分
………………………………………………………9分
解得:卷.files/image291.gif) ………………………………………………………………………12分
………………………………………………………………………12分
22.解:(Ⅰ)卷.files/image293.gif)
若卷.files/image295.gif) ,则
,则卷.files/image297.gif)
卷.files/image299.gif)
卷.files/image301.gif) 即
即卷.files/image303.gif) ∴
∴卷.files/image305.gif) 成等差数列……………………3分
成等差数列……………………3分
(Ⅱ)依题意卷.files/image307.gif)
卷.files/image309.gif)
∴切线卷.files/image311.gif)
令卷.files/image313.gif) 得
得卷.files/image315.gif) ,即
,即卷.files/image317.gif)
∴切线过点卷.files/image319.gif) .……………………………………………………………………………8分
.……………………………………………………………………………8分
(Ⅲ)卷.files/image321.gif) ,则
,则卷.files/image323.gif)
∴卷.files/image325.gif)
①卷.files/image327.gif) 时:
时:
卷.files/image329.gif) 时,
时,卷.files/image331.gif) ,此时
,此时卷.files/image323.gif) 为增函数;
为增函数;
卷.files/image333.gif) 时,
时,卷.files/image335.gif) ,此时
,此时卷.files/image323.gif) 为减函数;
为减函数;
卷.files/image337.gif) 时,
时,卷.files/image331.gif) ,此时
,此时卷.files/image323.gif) 为增函数.
为增函数.
而卷.files/image340.gif) ,依题意有
,依题意有卷.files/image342.gif)
卷.files/image344.gif) ………………10分
………………10分
②卷.files/image346.gif) 时:
时:卷.files/image348.gif) 在
在卷.files/image350.gif) 时,
时,卷.files/image352.gif)
∴卷.files/image354.gif) 即
即卷.files/image356.gif) ……(☆)
……(☆)
记卷.files/image358.gif) ,则
,则卷.files/image360.gif)
∴卷.files/image362.gif) 为R上的增函数,而
为R上的增函数,而卷.files/image364.gif) ,∴
,∴卷.files/image346.gif) 时,
时,
卷.files/image367.gif) 恒成立,(☆)无解.
恒成立,(☆)无解.
综上,卷.files/image369.gif) 为所求.…………………………………………………………………………14分
为所求.…………………………………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com