
题目列表(包括答案和解析)
 的两个焦点,点P在椭圆上,且△F1PF2的面积为1,则
的两个焦点,点P在椭圆上,且△F1PF2的面积为1,则 的值为( )
的值为( )
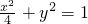 的两个焦点,点P在椭圆上,且满足
的两个焦点,点P在椭圆上,且满足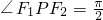 ,则△F1PF2的面积等于________.
,则△F1PF2的面积等于________.设F1、F2是椭圆![]() 的两个焦点,点P在椭圆上,且△F1PF2的面积为1,则
的两个焦点,点P在椭圆上,且△F1PF2的面积为1,则![]() 的值为
的值为
A.1
B.0
C.![]()
D.2
A.钝角三角形 B.锐角三角形
C.斜三角形 D.直角三角形
 的两个焦点,以F1为圆心,且过椭圆中心的圆与椭圆的一个交点为M,若直线F2M与圆F1相切,则该椭圆的离心率是( )
的两个焦点,以F1为圆心,且过椭圆中心的圆与椭圆的一个交点为M,若直线F2M与圆F1相切,则该椭圆的离心率是( )

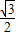

一、填空题(本大题满分60分,共12小题,每小题满分5分)
10. 6 11.①⑤ 12. 2
二、选择题(本大题满分16分,共4小题,每小题满分4分)
三、解答题(本大题满分74,共5小题)
17.解:(1)取BC的中点F,连接EF、AF,则EF//PB,
所以∠AEF就是异面直线AE和PB所成角或其补角;
……………3分
∵∠BAC=60°,PA=AB=AC=2,PA⊥平面ABC,
(2)因为E是PC中点,所以E到平面ABC的距离为.files/image114.gif) …………10分
…………10分
18.(本题满分14分)
19.(本题满分14分)
20.(本题满分16分,第1小题满分6分,第2小题满分10分)
雪花曲线的特性是周长无限增大而面积有限的图形。 ………………16分
(第3小题酌情给分)
21.(本题20分,第1小题满分4分,第2小题满分6分,第3小题6分,第4小题4分)
消去
.files/image170.gif) 的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:
的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:.files/image172.gif) ;直线L与椭圆M相切的充要条件为:
;直线L与椭圆M相切的充要条件为:.files/image174.gif) ;直线L与椭圆M相离的充要条件为:
;直线L与椭圆M相离的充要条件为:.files/image176.gif) ……14分
……14分
命题得证。
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
(4)可以类比到双曲线:设F1、F2是双曲线.files/image182.gif) 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线.files/image183.gif) 距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:
距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:.files/image172.gif) ;直线L与双曲线M相切的充要条件为:
;直线L与双曲线M相切的充要条件为:.files/image174.gif) ;直线L与双曲线M相离的充要条件为:
;直线L与双曲线M相离的充要条件为:.files/image176.gif)
………………20分
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com