
题目列表(包括答案和解析)
设关于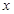 的方程
的方程
(1)若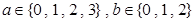 ,求方程有实根的概率;
,求方程有实根的概率;
(2)若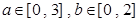 ,求方程有实根的概率.
,求方程有实根的概率.
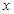 的方程
的方程
 ,求方程有实根的概率;
,求方程有实根的概率; ,求方程有实根的概率.
,求方程有实根的概率.
已知函数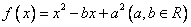
(1)若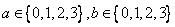 ,求方程
,求方程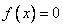 有实数根的概率;
有实数根的概率;
(2)若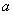 从区间
从区间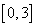 内任取一个数,
内任取一个数,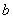 从区间
从区间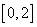 内任取一个数,求方程
内任取一个数,求方程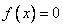 有实数根的概率。
有实数根的概率。
设集合![]() ,
,![]() ,
,![]() , 若
, 若![]() .
.
(Ⅰ) 求b = c的概率;
(Ⅱ)求方程![]() 有实根的概率.
有实根的概率.
设集合![]() ,
,![]() ,
,![]() , 若
, 若![]() .
.
(1) 求b = c的概率;
(2)求方程![]() 有实根的概率.
有实根的概率.
一.ADCDA, DBDAB, BA
 ;
15.3/10;
16.17/25
;
15.3/10;
16.17/25
三.解答题:
17.解:由已知 <0, 则
<0, 则 是第三或第四象限角. ………………2分
是第三或第四象限角. ………………2分
当 是第三象限角时,
是第三象限角时,  ,
,  ;………………5分
;………………5分
当 是第四象限角时,
是第四象限角时,  ,
,  .………………8分
.………………8分
18. 解:(1)0.7 ………………3分
(2) 0.6 ………………6分
(3) 他有可能是乘火车或轮船去, 他也有可能是乘汽车或飞机去. ………………9分
19.解:(Ⅰ)由直方图可知,参加本次竞赛的有:
4+6+8+7+5+2=32(人) ……………………3分
(Ⅱ)90分以上的人数为7+5=2=14(2分)
∴
即本次竞赛获奖率是43.75% ………………6分
(Ⅲ)参赛同学共有32人,按成绩排序后,第16,17个数是最中间两个。
即中位数落在80~90之间 ;
由直方图,落在80~90之间的人数最多,共8人。
所以众数也落在80~90之间。……………………9分
20. 解:(1) ;
;
 . ……………………3分
. ……………………3分
(2) 
 ………………6分
………………6分
(3)因 =
= ;
;  ,所以乙发挥的较稳定. ……………………9分
,所以乙发挥的较稳定. ……………………9分
21. 解:(1)略……………………3分
(2) ………………6分
………………6分
(3)当x=18时,  …………………9分
…………………9分
22.解:(b,c)的所有可能的取值有: (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), 4,6) ,(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6), 共36种。…………3分
(1)要使方程x2+bx+c=0有实根,必须满足△=b2-
(2,1), (3,1), (3,2), (4,1), (4,2), (4,3), (4,4), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6),共19种。
∴
方程x2+bx+c=0有实根的概率为 。 ……………6分
。 ……………6分
(2) 先后两次出现的点数中有5的可能结果有:(1,5), (2,5), (3,5), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,5), 共11种。其中使方程x2+bx+c=0有实根的结果有:(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,5), 共7种。
∴在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率为 。…………9分
。…………9分
(3) 试验的全部结束所构成的区域为 .
.
构成事件 的区域为
的区域为 .
.
所以所求的概率为p . ……………………………12分www.ks5u.com
. ……………………………12分www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com