
题目列表(包括答案和解析)
(本大题满分12分)
平面内有向量 ,点X为直线OP上的一动点。
,点X为直线OP上的一动点。
(1)当 取最小值时,求
取最小值时,求 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求 的值.
的值.
(本大题满分12分) 中角A的对边长等于2,向量
中角A的对边长等于2,向量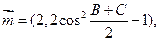 向量
向量 .
.
(1)当 取最大值时,求角A的大小;
取最大值时,求角A的大小;
(2)在(1)条件下,求 面积的最大值.
面积的最大值.
(本大题满分12分)设函数f(x)=x2+x-.
(1)若函数的定义域为[0,3],求f(x)的值域;
(2)若定义域为[a,a+1]时,f(x)的值域是[-,],求a的值.
(本大题满分12分)在△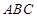 中,
中,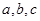 分别为内角
分别为内角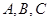 的对边,且
的对边,且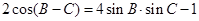
(1)求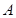
(2)若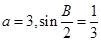 ,求
,求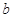
(本大题满分12分)已知点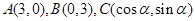
(1)若 ,求
,求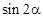 的值;
的值;
(2)若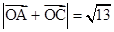 ,其中
,其中 是原点,且
是原点,且 ,求
,求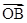 与
与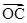 的夹角。
的夹角。
一.1、A,2、C,3、B,4、D,5、C,6、B,7、A,8、C,9、A,10、D
二.11、-3;.12、1;13、 14、
14、 15、
15、
三.16.解:
 ……(2’)
……(2’)
整理得: ……………………………(4’)
……………………………(4’)
又A为锐角, …………………(6’)
…………………(6’)
(2)由(1)知 ………………………(7’)
………………………(7’)
故

……………………………(12’)
当B=600时,Y取得最大值。……………………(13’)
17. 设答对题的个数为y,得分为 ,y=0,1,2,4 ,
,y=0,1,2,4 , =0,2,4,8………(1’)
=0,2,4,8………(1’)
∵ ,
,
 ,
,
|