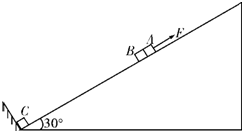（2010?丰台区一模）如图所示，可视为质点的物块A、B、C放在倾角为θ=37°、长L=2.0m的固定斜面上，物块与斜面间的动摩擦因数μ=0.5，A与B紧靠在一起，C紧靠在固定挡板上，物块的质量分别为m_A=0.8kg、m_B=0.4kg，其中A不带电，B、C的带电量分别为q B=+4.0×10-5C、q C =+2.0×10-5C，且保持不变，开始时三个物块均能保持静止且与斜面间均无摩擦力作用．如果选定两点电荷在相距无穷远处的电势能为0，则相距为r时，两点电荷具有的电势能可表示为E p=k

q1q2

r

．现给A施加一平行于斜面向上的力F，使A在斜面上做加速度大小为a=2.5m/s²的匀加速直线运动，经过时间t₀物体A、B分离并且力F变为恒力．当A运动到斜面顶端时撤去力F．已知静电力常量k=9.0×10⁹N?m²/C²，g=10m/s²，sin37°=0.6，cos37°=0.8．求：
（1）未施加力F时物块B、C间的距离；
（2）t₀时间内库仑力做的功；
（3）力F对A物块做的总功．

（2011?丰台区一模）1932年美国物理学家劳伦斯发明了回旋加速器，巧妙地利用带电粒子在磁场中的运动特点，解决了粒子的加速问题．现在回旋加速器被广泛应用于科学研究和医学设备中．

某型号的回旋加速器的工作原理如图甲所示，图为俯视图乙．回旋加速器的核心部分为D形盒，D形盒装在真空容器中，整个装置放在巨大的电磁铁两极之间的强大磁场中，磁场可以认为是匀强在场，且与D形盒盒面垂直．两盒间狭缝很小，带电粒子穿过的时间可以忽略不计．D形盒半径为R，磁场的磁感应强度为B．设质子从粒子源A处时入加速电场的初速度不计．质子质量为m、电荷量为+q．加速器接一定涉率高频交流电源，其电压为U．加速过程中不考虑相对论效应和重力作用．
（1）求质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r₁；
（2）求质子从静止开始加速到出口处所需的时间t；
（3）如果使用这台回旋加速器加速α粒子，需要进行怎样的改动？请写出必要的分析及推理．

（2008?丰台区一模）如图所示，光滑的圆弧轨道AB、EF，半径AO、O′F均为R且水平．质量为m、长度也为R的小车静止在光滑水平面CD上，小车上表面与轨道AB、EF的末端B、E相切．一质量为m的物体（可视为质点）从轨道AB的A点由静止下滑，由末端B滑上小车，小车立即向右运动．当小车右端与壁DE刚接触时，物体m恰好滑动到小车右端且相对于小车静止，同时小车与壁DE相碰后立即停止运动但不粘连，物体继续运动滑上圆弧轨道EF，以后又滑下来冲上小车．求：

（1）水平面CD的长度和物体m滑上轨道EF的最高点相对于E点的高度h；
（2）当物体再从轨道EF滑下并滑上小车后，小车立即向左运动．如果小车与壁BC相碰后速度也立即变为零，最后物体m停在小车上的Q点，则Q点距小车右端多远？

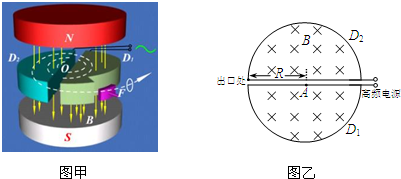
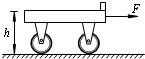（2009?丰台区模拟）如图所示，一辆平板小车静止在水平地面上，小车的右端放置一物块（可视为质点）．已知小车的质量M=4.0kg，长度l=1.0m，其上表面离地面的高度h=0.80m．物块的质量m=1.0kg，它与小车平板间的动摩擦因数μ=0.20，最大静摩擦力可以认为等于滑动摩擦力．若用水平向右的恒定拉力F=18N拉小车，经过一段时间后，物块从小车左端滑出，在物块滑出瞬间撤掉拉力F，不计小车与地面间的摩擦． 取g=10m/s²，求：
（1）拉动小车过程中拉力F所做的功；
（2）物块落地时的动能；
（3）物块落地时，物块与小车左端的水平距离．