题目列表(包括答案和解析)
对于数列
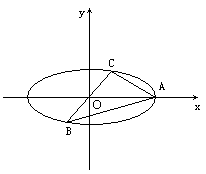
{an}，如果存在确定的正整数T，使得an+T＝an对一切正整数n都成立，则称数列{an}是以T为周期的周期数列．若一个周期数列{an}满足an+2＝an+1－an，n∈N+，且a1＝1，a2＝2，求a200，a2009．已知A，B，C是长轴长为4的椭圆上的三个点，点A是长轴的一个顶点，BC过椭圆中心O，如图，且
＝0，|BC|＝2|AC|．
(1)求椭圆的方程；
(2)如果椭圆上两点P，Q使∠PCQ的平分线垂直AO，则是否存在实数λ，使
＝λ
？请说明理由．
对于数列{an}，如果存在确定的正整数T，使得an+T＝an对一切正整数n都成立，则称数列{an}是以T为周期的周期数列．若一个周期数列{an}满足an+2＝an+1－an，n∈N+，且a1＝1，a2＝2，求a200，a2009．
已知函数f(x)，如果存在给定的实数对(a，b)，使得f(a＋x)·f(a－x)＝b恒成立，则称f(x)为“S－函数”．
(Ⅰ)判断函数f1(x)＝x，f2(x)＝3x是否是“S－函数”；
(Ⅱ)若f3(x)＝tanx是一个“S－函数”，求出所有满足条件的有序实数对(a，b)；
(Ⅲ)若定义域为R的函数f(x)是“S－函数”，且存在满足条件的有序实数对(0，1)和(1，1)，当x∈[0，1]时，f(x)的值域为[1，2]，求当x∈[－2012，2012]时函数f(x)的值域．
对于函数
，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点．如果函数f(x)＝
有且仅有两个不动点0和2．
(Ⅰ)试求b、c满足的关系式；
(Ⅱ)若c＝2时，各项不为零的数列{an}满足4Sn·f(
)＝1，
求证：
＜
＜
；
(Ⅲ)设bn＝－，Tn为数列{bn}的前n项和，求证：T2009－1＜ln2009＜T2008．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com