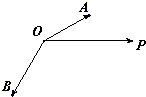
例1.如图..为单位向量.与夹角为1200. 与的夹角为450.||=5.用.表示. 解题思路分析: 以.为邻边.为对角线构造平行四边形 把向量在.方向上进行分解.如图.设=λ.=μ.λ>0.μ>0 则=λ+μ ∵ ||=||=1 ∴ λ=||.μ=|| △OEC中.∠E=600.∠OCE=750.由得: ∴ ∴ 说明:用若干个向量的线性组合表示一个向量.是向量中的基本而又重要的问题.通常通过构造平行四边形来处理 例2.已知△ABC中.A.BC边上的高为AD.求点D和向量坐标. 解题思路分析: 用解方程组思想 设D(x.y).则= ∵=.·=0 ∴ -6=0.即2x+y-3=0 ① ∵=.∥ ∴ -6.即x-2y+1=0 ② 由①②得: ∴ D(1.1).= 例3.求与向量=.-1)和=(1.)夹角相等.且模为的向量的坐标. 解题思路分析: 用解方程组思想 法一:设=(x.y).则·=x-y.·=x+y ∵ <.>=<.> ∴ ∴ 即 ① 又||= ∴ x2+y2=2 ② 由①②得 或(舍) ∴= 法二:从分析形的特征着手 ∵ ||=||=2 ·=0 ∴ △AOB为等腰直角三角形.如图 ∵ ||=.∠AOC=∠BOC ∴ C为AB中点 ∴ C() 说明:数形结合是学好向量的重要思想方法.分析图中的几何性质可以简化计算. 例4.在△OAB的边OA.OB上分别取点M.N.使||∶||=1∶3.||∶||=1∶4.设线段AN与BM交于点P.记= .=.用 .表示向量. 解题思路分析: ∵ B.P.M共线 ∴ 记=s ∴ ① 同理.记 ∴ = ② ∵ ,不共线 ∴ 由①②得解之得: ∴ 说明:从点共线转化为向量共线.进而引入参数是常用技巧之一.平面向量基本定理是向量重要定理之一.利用该定理唯一性的性质得到关于s.t的方程. 例5.已知长方形ABCD.AB=3.BC=2.E为BC中点.P为AB上一点 (1)利用向量知识判定点P在什么位置时.∠PED=450, (2)若∠PED=450.求证:P.D.C.E四点共圆. 解题思路分析: 利用坐标系可以确定点P位置 如图.建立平面直角坐标系 则C 设P(0.y) ∴ =(1.3).= ∴ ·=3y-1 代入cos450= 解之得(舍).或y=2 ∴ 点P为靠近点A的AB三等分处 (3)当∠PED=450时.由 ∴ =(2.1).= ∴·=0 ∴ ∠DPE=900 又∠DCE=900 ∴ D.P.E.C四点共圆 说明:利用向量处理几何问题一步要骤为:①建立平面直角坐标系,②设点的坐标,③求出有关向量的坐标,④利用向量的运算计算结果,⑤得到结论. 【
查看更多】
题目列表(包括答案和解析)
、如图,
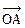
,
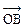
为单位向量,
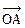
与
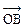
夹角为120
0,
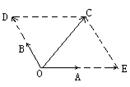
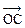
与
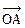
的夹角为45
0,|
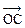
|=5,用
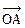
,
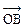
表示
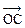
。
查看答案和解析>>
如图,已知单位向量
、
与向量
共面,且夹角分别
为
和
,设
=
-
,则向量
与
的夹角是
.
查看答案和解析>>
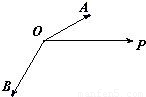
如图,已知单位向量
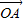
、
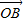
与向量
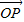
共面,且夹角分别
为
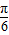
和
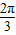
,设
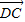
=
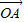
-
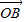
,则向量
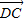
与
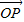
的夹角是
.
查看答案和解析>>
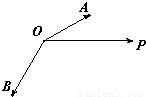
如图,已知单位向量
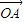
、
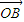
与向量
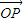
共面,且夹角分别
为
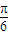
和
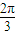
,设
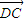
=
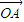
-
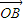
,则向量
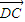
与
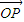
的夹角是
.
查看答案和解析>>

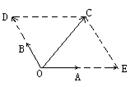 、如图,
、如图,![]() ,
,![]() 为单位向量,
为单位向量,![]() 与
与![]() 夹角为1200,
夹角为1200,![]() 与
与![]() 的夹角为450,|
的夹角为450,|![]() |=5,用
|=5,用![]() ,
,![]() 表示
表示![]() 。
。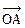 ,
,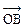 为单位向量,
为单位向量,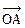 与
与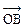 夹角为1200,
夹角为1200,
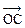 与
与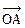 的夹角为450,|
的夹角为450,|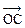 |=5,用
|=5,用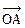 ,
,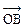 表示
表示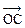 。
。 如图,已知单位向量
如图,已知单位向量 如图,已知单位向量
如图,已知单位向量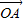 、
、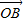 与向量
与向量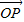 共面,且夹角分别
共面,且夹角分别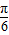 和
和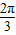 ,设
,设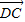 =
=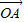 -
-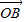 ,则向量
,则向量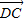 与
与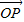 的夹角是 .
的夹角是 . 如图,已知单位向量
如图,已知单位向量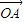 、
、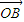 与向量
与向量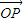 共面,且夹角分别
共面,且夹角分别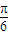 和
和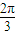 ,设
,设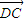 =
=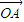 -
-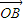 ,则向量
,则向量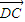 与
与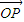 的夹角是 .
的夹角是 .