
题目列表(包括答案和解析)
在极坐标系中,圆 :
: 和直线
和直线 相交于
相交于 、
、 两点,求线段
两点,求线段 的长
的长
【解析】本试题主要考查了极坐标系与参数方程的运用。先将圆的极坐标方程圆 :
: 即
即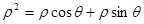 化为直角坐标方程即
化为直角坐标方程即 
然后利用直线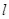
 即
即 ,得到圆心到直线的距离
,得到圆心到直线的距离 ,从而利用勾股定理求解弦长AB。
,从而利用勾股定理求解弦长AB。
解:分别将圆 和直线
和直线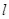 的极坐标方程化为直角坐标方程:
的极坐标方程化为直角坐标方程:
圆 :
: 即
即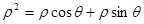 即
即  ,
,
即 , ∴ 圆心
, ∴ 圆心 ,
, ---------3分
---------3分
直线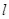
 即
即 , ------6分
, ------6分
则圆心 到直线
到直线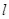 的距离
的距离 ,----------8分
,----------8分
则 即所求弦长为
即所求弦长为
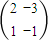 所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.
所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.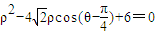 .
.
(共12分)(考生在下面两题中任选一题解答,若多选则安所做的第一题计分)
选修4—4:坐标系与参数方程
1:已知曲线C的极坐标方程是 ,设直线
,设直线 的参数方程是
的参数方程是 (
( 为参数)。
为参数)。
(1)将曲线C的极坐标方程转化为直角坐标方程;
(2)设直线 与
与 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
(共12分)(考生在下面两题中任选一题解答,若多选则安所做的第一题计分)
选修4—4:坐标系与参数方程
1:已知曲线C的极坐标方程是 ,设直线
,设直线 的参数方程是
的参数方程是 (
( 为参数)。
为参数)。
(1)将曲线C的极坐标方程转化为直角坐标方程;
(2)设直线 与
与 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
| π |
| 4 |
| ||
| 2 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com