
题目列表(包括答案和解析)
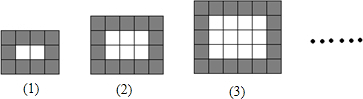
| 图形编号 | (1) | (2) | (3) | (4) | … |
| 黑色瓷砖的块数 | 10 | 14 | 18 | 22 22 |
… |
| 白色瓷砖的块数 | 2 | 6 | 12 | 20 20 |
… |
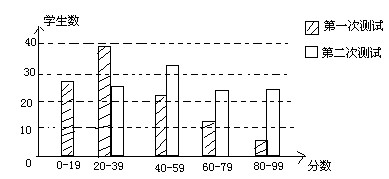 26、有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
26、有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.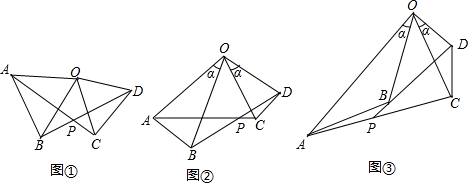
有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
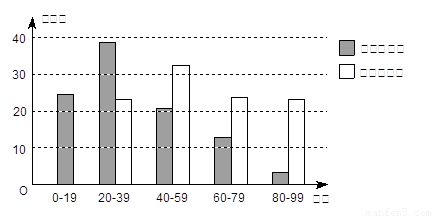
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上);
(1)两次测试最低分在第 次测试中;
(2)第 次测试较容易;
(3)第一次测试中,中位数在 分数段,第二次测试中,中位数在 分数段.
一、选择题:
二、填空题:
9. 2
10.  11.
11.  12.
12.  ,
, .
.
三、解答题;
13.原式=-4+ +3+2
+3+2 ……………..4分
……………..4分
=3 -1………………………..5分
-1………………………..5分
14.原式=3(a+1)-(a-1) ………………..1分
=
=
当a= -2时,原式=2(
-2时,原式=2( -2+2)=2
-2+2)=2 ….5分
….5分
15. 去分母得 x-1>3(5-x)
去括号得 x-1>15-3x ………………1分
移项得 x+3x>15+1 ………………2分
合并同类项得 4x>16 ……………….3分
系数化为1得 x>4 …………………4分
这个不等式的解集在数轴上表示:
 |
…………5分
16.证明:∵四边形ABCD是平行四边形
 ∴AB∥CD且AB=CD… 1分
∴AB∥CD且AB=CD… 1分
∴∠ABE=∠CDF……… 2分
又∵AE⊥BD,CF⊥BD
∴∠AEB=∠CFD=900… 3分
∴Rt△ABE≌Rt△CDF… 4分
∴∠BAE=∠DCF……… .5分
17. 设服装厂原来每天加工 套演出服.
套演出服.
根据题意,得 . …. 2分
. …. 2分
解得
 .…………………………….3分
.…………………………….3分
经检验, 是原方程的根.……… .4分
是原方程的根.……… .4分
答:服装厂原来每天加工20套演出服 ..5分
18. 依题意得,直线l的解析式为y=x. ………………………………………..2分
∵A(a,3)在直线y= x上,
∴a=3,即A(3,3). …………………………………………………………3分
又∵A(3,3)在 的图像上,可求得k=9. ………………………………4分
的图像上,可求得k=9. ………………………………4分
所以反比例函数的解析式为: ………………………………….….5分
………………………………….….5分

 19. (1)
19. (1)
 (2)
(2)

20.在 中,
中,
 .
.
 ……………. 2分
……………. 2分
在 中,
中,

 …………3分
…………3分
 烟囱高
烟囱高 ……………………….4分
……………………….4分
 ,
,
 这棵大树不会被歪倒的烟囱砸着. ……………………………..5分
这棵大树不会被歪倒的烟囱砸着. ……………………………..5分
21. (1)
∴选出的恰好是“每天锻炼超过1小时”的学生的概率是 .
1分
.
1分
(2)720×(1- )-120-20=400(人)
)-120-20=400(人)
∴“没时间”的人数是400人. 2分
补全频数分布直方图略. 3分
(3)4.3×(1- )=3.225(万人)
)=3.225(万人)
∴2008年全州初中毕业生每天锻炼未超过1小时约有3.225万人. 4分
(4)说明:内容健康,能符合题意即可. 5分
22.(1) +1或
+1或 -1 ………………………………………….. 2分
-1 ………………………………………….. 2分
(2)45
 或
或

 ………………………..5分
………………………..5分
23.当a=0时,原方程为
 ,解得
,解得 ,
,
即原方程无整数解. ……………1分
当 时,方程为一元二次方程,它至少有一个整数根,
时,方程为一元二次方程,它至少有一个整数根,
说明判别式 为完全平方数, ……2分
为完全平方数, ……2分
从而 为完全平方数,设
为完全平方数,设 ,则
,则 为正奇数,且
为正奇数,且 否则(
否则( ),
),
所以, .
.
由求根公式得 
所以 
 …………….. 5分
…………….. 5分
要使 为整数,而
为整数,而 为正奇数,只能
为正奇数,只能 ,从而
,从而 ; ……. 6分
; ……. 6分
要使 为整数,
为整数, 可取1,5,7,从而
可取1,5,7,从而 ………7分
………7分
综上所述, 的值为
的值为

 24.(1)由题意,得
24.(1)由题意,得 ,……………..1分
,……………..1分
解得


 抛物线的解析式为
抛物线的解析式为
(2)如图1,当 在运动过程中,存在
在运动过程中,存在 与坐标轴相切的情况。
与坐标轴相切的情况。
设点P坐标为 ,则当
,则当 与y轴相切时,
与y轴相切时,
有 =1,
=1,  =
= 1.
1.
由 =-1,得
=-1,得 =
= .
.

 .
.
由 得
得




当 与
与 轴相切时有
轴相切时有 ,
,
 抛物线开口向上,且顶点在
抛物线开口向上,且顶点在 轴的上方,
轴的上方,




由 得
得
解得 2,
2,
综上所述,符合要求的圆心P有三个,其坐标分别为:
 ,
, …………………………………4分
…………………………………4分
(3)设点Q坐标为
 ,则当
,则当 与两条坐标轴都相切时,有
与两条坐标轴都相切时,有 .
.
由 ,得
,得 ,
,
即
解得
由
 ,得
,得 .
.
即 此方程无解.
此方程无解.

 O的半径为
O的半径为
 ………………………7分
………………………7分
25. (1)EN与MF的数量关系为:EN=MF;. ………1分
(2)EN与MF的相等关系依然成立.
 证明:连接DE、DF(见图2)
证明:连接DE、DF(见图2)
 D、E分别是AB、AC的中点,
D、E分别是AB、AC的中点,
 DE
DE BC,DE=
BC,DE= BC,同理DF
BC,同理DF AC,DF=
AC,DF= AC.
AC.

 是等边三角形,
是等边三角形,
 BC=AC,
BC=AC, DE=DF.
DE=DF.



 ,
,
 ,
,

 是等边三角形,
是等边三角形,
 DN=DM,
DN=DM, 


 ………………………………..6分
………………………………..6分
(3)EN与MF的相等关系仍然成立. ……………… ……….7分
图形正确1分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com