把一枚骰子抛6次，设正面出现的点数为x，

（1）求出x的可能取值情况（即全体基本事件）；

（2）下列事件由哪些基本事件组成（用x的取值回答）.

①x的取值为2的倍数（记为事件A）；

②x的取值大于3（记为事件B）；

③x的取值不超过2（记为事件C）；

④x的取值是质数（记为事件D）.

（3）判断上述事件是否为古典概型，并求出其概率.

下列随机试验是否属于古典概型？(1) 将一只黑球、一只白球随机地放入4个不同的盒子里；(2) 某射手一次射击命中的环数；(3) 在一小时内，某电话总机接到的呼叫次数;(4)把一枚图钉扔在地上，它可以针尖朝上，也可以针尖朝下.

判断下列概率模型是古典概型还是几何概型？

(1)如图3-3-4,转盘上有8个面积相等的扇形,转动转盘,求转盘停止转动时指针落在阴影部分的概率.

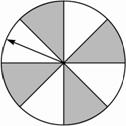
        图3-3-4

(2)在500 mL的水中有一个草履虫,现从中随机取出2 mL水样放到显微镜下观察,求发现草履虫的概率.

某中学研究性学习小组，为了考察高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了 50名学生.调査结果表明：在爱看课外书的25人中有18人作文水平好，另7人作文水平一般；在不爱看课外书的25人中有6人作文水平好，另19人作文水平一般.

（Ⅰ）试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？

高中学生的作文水平与爱看课外书的2×2列联表

	爱看课外书	不爱看课外书	总计
作文水平好
作文水平一般
总计

（Ⅱ）将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5，某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.

参考公式：，其中.

参考数据：

	0.10	0.05	0.025	0.010	0.005	0.001
	2.706	3.841	5.024	6.635	7.879	10.828

【解析】本试题主要考查了古典概型和列联表中独立性检验的运用。结合公式为判定两个分类变量的相关性，

第二问中，确定

结合互斥事件的概率求解得到。

解：因为2×2列联表如下

	爱看课外书	不爱看课外书	总计
作文水平好	18	6	24
作文水平一般	7	19	26
总计	25	25	50

 

下列概率模型中，古典概型的个数为(　　)

(1)从区间[1,10]内任取一个数，求取到1的概率；

(2)从1,2，…，9,10中任取一个整数，求取到1的概率；

(3)向一个正方形ABCD内任意投一点P，求点P刚好与点A重合的概率；

(4)向上抛掷一枚质地不均匀的硬币，求出现反面朝上的概率．

A．1　　　　　　　　　　　      B．2

C．3                            D．4