A.(选修模块3-3)

(1)若一气泡从湖底上升到湖面的过程中温度保持不变,则在此过程中关于气泡中的气体,下列说法中正确的是____________.(填写选项前的字母)

A.气体分子间的作用力增大                      B.气体分子的平均速率增大

C.气体分子的平均动能减小                      D.气体组成的系统的熵增加

(2)若将气泡内的气体视为理想气体,气泡从湖底上升到湖面的过程中,对外界做了0.6 J的功,则此过程中气泡____________(填“吸收”或“放出”)的热量是____________J.气泡到达湖面后,温度上升的过程中,又对外界做了0.1 J的功,同时吸收了0.3 J的热量,则此过程中,气泡内气体内能增加了____________J.

(3)已知气泡内气体的密度为1.29 kg/m³,平均摩尔质量为0.029 kg/mol.阿伏加德罗常数N_A=6.02×10²³mol^-1,取气体分子的平均直径为2×10^-10m.若气泡内的气体能完全变为液体,请估算液体体积与原来气体体积的比值.(结果保留一位有效数字)

B.(选修模块3-4)

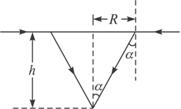
(1)如图甲所示,强强乘坐速度为0.9c(c为光速)的宇宙飞船追赶正前方的壮壮,壮壮的飞行速度为0.5c.强强向壮壮发出一束光进行联络,则壮壮观测到该光束的传播速度为___________.(填写选项前的字母)

甲

A.0.4c             B.0.5c             C.0.9c             D.1.0c

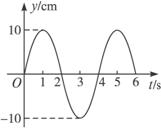
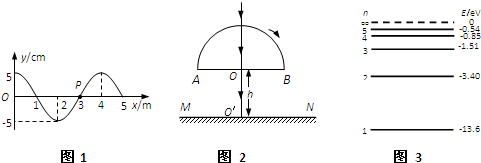
(2)在t=0时刻,质点A开始做简谐运动,其振动图象如图乙所示.质点A振动的周期是_________s;t=8 s时,质点A的运动沿y轴的_________方向(填“正”或“负”）;质点B在波的传播方向上与A相距16 m.已知波的传播速度为2 m/s,在t=9 s时,质点B偏离平衡位置的位移是_________cm.

乙

(3)图丙是北京奥运会期间安置在游泳池底部的照相机拍摄的一张照片,相机的镜头竖直向上.照片中,水立方运动馆的景象呈现在半径r=11 cm的圆形范围内,水面上的运动员手到脚的长度l=10 cm.若已知水的折射率,请根据运动员的实际身高估算该游泳池的水深h.(结果保留两位有效数字)

丙

C.(选修模块3-5)

    在β衰变中常伴有一种称为“中微子”的粒子放出,中微子的性质十分特别,因此在实验中很难探测.1953年,莱尼斯和柯文建造了一个由大水槽和探测器组成的实验系统,利用中微子与水中的核反应,间接地证实了中微子的存在.

(1)中微子与水中的发生核反应,产生中子()和正电子(),即

中微子+→

可以判定,中微子的质量数和电荷数分别是___________.(填写选项前的字母)

A.0和0                B.0和1                C.1和0                D.1和1

(2)上述核反应产生的正电子与水中的电子相遇,与电子形成几乎静止的整体后,可以转变为两个光子(γ),即

→2γ

已知正电子和电子的质量都为9.1×10^-31kg,反应中产生的每个光子的能量约为________J.正电子与电子相遇不可能只转变为一个光子,原因是________________________.

(3)试通过分析比较,具有相同动能的中子和电子的物质波波长的大小.

　　太阳是银河系中极为普通的一颗恒星，剧烈的热核反应使之不断地向外辐射能量，太阳辐射的能量绝大部分集中在紫外波段、可见光波段和红外光波段，它们的能量分别占总辐射量的9％，44％和47％．

　　地球的大气层中，基本不变的成分为氧、氮、氩等，占大气总量的99.96％，可变气体成分主要有、水汽和臭氧等，这些气体的含量极小，但对大气物理状况的影响极大．

　　大气臭氧层一般是指高度在离地面10km～15km的大气层，其中臭氧浓度很低，将它折合成标准状况，其总累积厚度也不过0.3cm，其含量虽小，但对地球的气候和生物影响很大，如臭氧层空洞每增加1％，人类患皮肤癌比率将增加2％～3％．

(1)大气压强p随距地面高度h(m)的增大而减小，经验公式为＝·，其中为地表的气压值，e＝2.718．若臭氧层集中在24km的高空处，设在该高度处的温度为－50℃，试估算臭氧层的厚度．

(2)设地球半径为R，在离地面20km～30km处的平均温度为，压强为，地球表面温度为2，大气压强为1×，请写出这部分臭氧全部集中在地表的厚度H的表达式．

(3)由于臭氧在紫外光波长200nm～300nm的谱段有强吸收带，在300nm～340nm的谱段有弱的吸收带，在440nm～740nm可见光区有吸收带，所以臭氧层可以大量吸收紫外线和可见光．

①紫外线产生的微观机理是

[　　]

  A．振荡电路中自由电子的运动而产生的

  B．原子的外层电子受到激发而产生的

  C．原子的内层电子受到激发而产生的

  D．原子核受到激发而产生的

②氢原子处于基态时能量为＝－13.6eV，它从n＝2能级向基态跃迁时，发生的紫外线波长为多少？(h＝6.63×J·s)

③若用上述两种波长的紫外光照射银板，试计算说明哪个谱段的光线可能使银板产生光电效应．(银的极限频率为1.15×Hz)

　　21世纪国际联合开发月球一项大型的国际航天合作计划重返月球将成为新的航空热点．人类在月球上生存首先要解决呼吸与饮用水的问题．淡水和氧气是人类生存必不可少的物质．月球上既没有水又没有空气，但月球的沙土里含有很多的氧，于是科学家提出了用月球的沙土制造水和氧气的设想．其次是月球基地建设必须保证食物供应．近几年，科学家在空间站进行了大量的生物学试验，先后培育了一百多种“太空植物”，实验证明在失重条件下，植物种子的发芽率更高，生长更快，开花或抽穗时间更早．科学家也对一些动物进行试验，证明在失重条件下不会影响新生命的诞生，最后是建立月球基地需要的能源问题．月球上没有风没有雨，晴朗无阴，终日有阳光照射，而且由于没有大气吸收，太阳的辐射强度大约是地球上的一倍半，因此月球上完全可以用太阳能来照明、供热、供暖、发电，当然必要时还可以在月球上建立核电站．

阅读上文回答下列问题：

(1)月球上科学家估计160t沙土含有15t至16t氧化铁：21%矿物，用从地球上带去的氢气还原氧化铁得到水，水电解制得氧气，一个人每年需0.1t氧气，问160t沙土最多可制得的氧气供多少人使用一年？

(2)未来人在月球基地上培育植物，植物生存的非生物因素是什么？设想一下植物所需水从何得来？写出光合作用的方程式，其中CO₂从何处得来？光合作用的氧气可供植物干什么？

(3)月球的重力加速度是地球的1/6，已知月球半径为1740km，地球的重力加速度为9.8m/s²，求地球人乘飞船到月球时速度多大？

(4)有一太阳能热水器，接受来自太阳的辐射能，使水升高温度，设阳光垂直照射到月球上传播方向上的光流强度为3.8×10³W/m²，热水器受阳光垂直照射的面积为1m²，认为阳光一直垂直照射热水器，且辐射太阳能的70%转化为水的内能，照射半小时，可使100kg水升高多少度？(已知c(H₂O)＝4.2×10³kJ/kg℃)

第八部分 静电场

第一讲 基本知识介绍

在奥赛考纲中，静电学知识点数目不算多，总数和高考考纲基本相同，但在个别知识点上，奥赛的要求显然更加深化了：如非匀强电场中电势的计算、电容器的连接和静电能计算、电介质的极化等。在处理物理问题的方法上，对无限分割和叠加原理提出了更高的要求。

如果把静电场的问题分为两部分，那就是电场本身的问题、和对场中带电体的研究，高考考纲比较注重第二部分中带电粒子的运动问题，而奥赛考纲更注重第一部分和第二部分中的静态问题。也就是说，奥赛关注的是电场中更本质的内容，关注的是纵向的深化和而非横向的综合。

一、电场强度

1、实验定律

a、库仑定律

内容；

条件：⑴点电荷，⑵真空，⑶点电荷静止或相对静止。事实上，条件⑴和⑵均不能视为对库仑定律的限制，因为叠加原理可以将点电荷之间的静电力应用到一般带电体，非真空介质可以通过介电常数将k进行修正（如果介质分布是均匀和“充分宽广”的，一般认为k′= k /ε_r）。只有条件⑶，它才是静电学的基本前提和出发点（但这一点又是常常被忽视和被不恰当地“综合应用”的）。

b、电荷守恒定律

c、叠加原理

2、电场强度

a、电场强度的定义

电场的概念；试探电荷（检验电荷）；定义意味着一种适用于任何电场的对电场的检测手段；电场线是抽象而直观地描述电场有效工具（电场线的基本属性）。

b、不同电场中场强的计算

决定电场强弱的因素有两个：场源（带电量和带电体的形状）和空间位置。这可以从不同电场的场强决定式看出——

⑴点电荷：E = k

结合点电荷的场强和叠加原理，我们可以求出任何电场的场强，如——

⑵均匀带电环，垂直环面轴线上的某点P：E = ，其中r和R的意义见图7-1。

⑶均匀带电球壳

内部：E_内 = 0

外部：E_外 = k ，其中r指考察点到球心的距离

如果球壳是有厚度的的（内径R₁ 、外径R₂），在壳体中（R₁＜r＜R₂）：

E =  ，其中ρ为电荷体密度。这个式子的物理意义可以参照万有引力定律当中（条件部分）的“剥皮法则”理解〔即为图7-2中虚线以内部分的总电量…〕。

⑷无限长均匀带电直线（电荷线密度为λ）：E = 

⑸无限大均匀带电平面（电荷面密度为σ）：E = 2πkσ

二、电势

1、电势：把一电荷从P点移到参考点P₀时电场力所做的功W与该电荷电量q的比值，即

U = 

参考点即电势为零的点，通常取无穷远或大地为参考点。

和场强一样，电势是属于场本身的物理量。W则为电荷的电势能。

2、典型电场的电势

a、点电荷

以无穷远为参考点，U = k

b、均匀带电球壳

以无穷远为参考点，U_外 = k ，U_内 = k

3、电势的叠加

由于电势的是标量，所以电势的叠加服从代数加法。很显然，有了点电荷电势的表达式和叠加原理，我们可以求出任何电场的电势分布。

4、电场力对电荷做功

W_AB = q（U_A － U_B）= qU_AB 

三、静电场中的导体

静电感应→静电平衡（狭义和广义）→静电屏蔽

1、静电平衡的特征可以总结为以下三层含义——

a、导体内部的合场强为零；表面的合场强不为零且一般各处不等，表面的合场强方向总是垂直导体表面。

b、导体是等势体，表面是等势面。

c、导体内部没有净电荷；孤立导体的净电荷在表面的分布情况取决于导体表面的曲率。

2、静电屏蔽

导体壳（网罩）不接地时，可以实现外部对内部的屏蔽，但不能实现内部对外部的屏蔽；导体壳（网罩）接地后，既可实现外部对内部的屏蔽，也可实现内部对外部的屏蔽。

四、电容

1、电容器

孤立导体电容器→一般电容器

2、电容

a、定义式 C = 

b、决定式。决定电容器电容的因素是：导体的形状和位置关系、绝缘介质的种类，所以不同电容器有不同的电容

⑴平行板电容器 C =  =  ，其中ε为绝对介电常数（真空中ε₀ =  ，其它介质中ε= ），ε_r则为相对介电常数，ε_r =  。

⑵柱形电容器：C = 

⑶球形电容器：C = 

3、电容器的连接

a、串联  = +++ … +

b、并联 C = C₁ + C₂ + C₃ + … + C_n 

4、电容器的能量

用图7-3表征电容器的充电过程，“搬运”电荷做功W就是图中阴影的面积，这也就是电容器的储能E ，所以

E = q₀U₀ = C = 

电场的能量。电容器储存的能量究竟是属于电荷还是属于电场？正确答案是后者，因此，我们可以将电容器的能量用场强E表示。

对平行板电容器 E_总 = E² 

认为电场能均匀分布在电场中，则单位体积的电场储能 w = E² 。而且，这以结论适用于非匀强电场。

五、电介质的极化

1、电介质的极化

a、电介质分为两类：无极分子和有极分子，前者是指在没有外电场时每个分子的正、负电荷“重心”彼此重合（如气态的H₂ 、O₂ 、N₂和CO₂），后者则反之（如气态的H₂O 、SO₂和液态的水硝基笨）

b、电介质的极化：当介质中存在外电场时，无极分子会变为有极分子，有极分子会由原来的杂乱排列变成规则排列，如图7-4所示。

2、束缚电荷、自由电荷、极化电荷与宏观过剩电荷

a、束缚电荷与自由电荷：在图7-4中，电介质左右两端分别显现负电和正电，但这些电荷并不能自由移动，因此称为束缚电荷，除了电介质，导体中的原子核和内层电子也是束缚电荷；反之，能够自由移动的电荷称为自由电荷。事实上，导体中存在束缚电荷与自由电荷，绝缘体中也存在束缚电荷和自由电荷，只是它们的比例差异较大而已。

b、极化电荷是更严格意义上的束缚电荷，就是指图7-4中电介质两端显现的电荷。而宏观过剩电荷是相对极化电荷来说的，它是指可以自由移动的净电荷。宏观过剩电荷与极化电荷的重要区别是：前者能够用来冲放电，也能用仪表测量，但后者却不能。

第二讲 重要模型与专题

一、场强和电场力

【物理情形1】试证明：均匀带电球壳内部任意一点的场强均为零。

【模型分析】这是一个叠加原理应用的基本事例。

如图7-5所示，在球壳内取一点P ，以P为顶点做两个对顶的、顶角很小的锥体，锥体与球面相交得到球面上的两个面元ΔS₁和ΔS₂ ，设球面的电荷面密度为σ，则这两个面元在P点激发的场强分别为

ΔE₁ = k

ΔE₂ = k

为了弄清ΔE₁和ΔE₂的大小关系，引进锥体顶部的立体角ΔΩ ，显然

 = ΔΩ = 

所以 ΔE₁ = k ，ΔE₂ = k ，即：ΔE₁ = ΔE₂ ，而它们的方向是相反的，故在P点激发的合场强为零。

同理，其它各个相对的面元ΔS₃和ΔS₄ 、ΔS₅和ΔS₆ … 激发的合场强均为零。原命题得证。

【模型变换】半径为R的均匀带电球面，电荷的面密度为σ，试求球心处的电场强度。

【解析】如图7-6所示，在球面上的P处取一极小的面元ΔS ，它在球心O点激发的场强大小为

ΔE = k ，方向由P指向O点。

无穷多个这样的面元激发的场强大小和ΔS激发的完全相同，但方向各不相同，它们矢量合成的效果怎样呢？这里我们要大胆地预见——由于由于在x方向、y方向上的对称性，Σ = Σ = 0 ，最后的ΣE = ΣE_z ，所以先求

ΔE_z = ΔEcosθ= k ，而且ΔScosθ为面元在xoy平面的投影，设为ΔS′

所以 ΣE_z = ΣΔS′

而 ΣΔS′= πR² 

【答案】E = kπσ ，方向垂直边界线所在的平面。

〖学员思考〗如果这个半球面在yoz平面的两边均匀带有异种电荷，面密度仍为σ，那么，球心处的场强又是多少？

〖推荐解法〗将半球面看成4个球面，每个球面在x、y、z三个方向上分量均为 kπσ，能够对称抵消的将是y、z两个方向上的分量，因此ΣE = ΣE_x …

〖答案〗大小为kπσ，方向沿x轴方向（由带正电的一方指向带负电的一方）。

【物理情形2】有一个均匀的带电球体，球心在O点，半径为R ，电荷体密度为ρ ，球体内有一个球形空腔，空腔球心在O′点，半径为R′，= a ，如图7-7所示，试求空腔中各点的场强。

【模型分析】这里涉及两个知识的应用：一是均匀带电球体的场强定式（它也是来自叠加原理，这里具体用到的是球体内部的结论，即“剥皮法则”），二是填补法。

将球体和空腔看成完整的带正电的大球和带负电（电荷体密度相等）的小球的集合，对于空腔中任意一点P ，设 = r₁ ， = r₂ ，则大球激发的场强为

E₁ = k = kρπr₁ ，方向由O指向P

“小球”激发的场强为

E₂ = k = kρπr₂ ，方向由P指向O′

E₁和E₂的矢量合成遵从平行四边形法则，ΣE的方向如图。又由于矢量三角形PE₁ΣE和空间位置三角形OP O′是相似的，ΣE的大小和方向就不难确定了。

【答案】恒为kρπa ，方向均沿O → O′，空腔里的电场是匀强电场。

〖学员思考〗如果在模型2中的OO′连线上O′一侧距离O为b（b＞R）的地方放一个电量为q的点电荷，它受到的电场力将为多大？

〖解说〗上面解法的按部就班应用…

〖答〗πkρq〔?〕。

二、电势、电量与电场力的功

【物理情形1】如图7-8所示，半径为R的圆环均匀带电，电荷线密度为λ，圆心在O点，过圆心跟环面垂直的轴线上有P点， = r ，以无穷远为参考点，试求P点的电势U_P 。

【模型分析】这是一个电势标量叠加的简单模型。先在圆环上取一个元段ΔL ，它在P点形成的电势

ΔU = k

环共有段，各段在P点形成的电势相同，而且它们是标量叠加。

【答案】U_P = 

〖思考〗如果上题中知道的是环的总电量Q ，则U_P的结论为多少？如果这个总电量的分布不是均匀的，结论会改变吗？

〖答〗U_P =  ；结论不会改变。

〖再思考〗将环换成半径为R的薄球壳，总电量仍为Q ，试问：（1）当电量均匀分布时，球心电势为多少？球内（包括表面）各点电势为多少？（2）当电量不均匀分布时，球心电势为多少？球内（包括表面）各点电势为多少？

〖解说〗（1）球心电势的求解从略；

球内任一点的求解参看图7-5

ΔU₁ = k= k·= kσΔΩ

ΔU₂ = kσΔΩ

它们代数叠加成 ΔU = ΔU₁ + ΔU₂ = kσΔΩ

而 r₁ + r₂ = 2Rcosα

所以 ΔU = 2RkσΔΩ

所有面元形成电势的叠加 ΣU = 2RkσΣΔΩ

注意：一个完整球面的ΣΔΩ = 4π（单位：球面度sr），但作为对顶的锥角，ΣΔΩ只能是2π ，所以——

ΣU = 4πRkσ= k

（2）球心电势的求解和〖思考〗相同；

球内任一点的电势求解可以从（1）问的求解过程得到结论的反证。

〖答〗（1）球心、球内任一点的电势均为k ；（2）球心电势仍为k ，但其它各点的电势将随电量的分布情况的不同而不同（内部不再是等势体，球面不再是等势面）。

【相关应用】如图7-9所示，球形导体空腔内、外壁的半径分别为R₁和R₂ ，带有净电量+q ，现在其内部距球心为r的地方放一个电量为+Q的点电荷，试求球心处的电势。

【解析】由于静电感应，球壳的内、外壁形成两个带电球壳。球心电势是两个球壳形成电势、点电荷形成电势的合效果。

根据静电感应的尝试，内壁的电荷量为－Q ，外壁的电荷量为+Q+q ，虽然内壁的带电是不均匀的，根据上面的结论，其在球心形成的电势仍可以应用定式，所以…

【答案】U_o = k － k + k 。

〖反馈练习〗如图7-10所示，两个极薄的同心导体球壳A和B，半径分别为R_A和R_B ，现让A壳接地，而在B壳的外部距球心d的地方放一个电量为+q的点电荷。试求：（1）A球壳的感应电荷量；（2）外球壳的电势。

〖解说〗这是一个更为复杂的静电感应情形，B壳将形成图示的感应电荷分布（但没有净电量），A壳的情形未画出（有净电量），它们的感应电荷分布都是不均匀的。

此外，我们还要用到一个重要的常识：接地导体（A壳）的电势为零。但值得注意的是，这里的“为零”是一个合效果，它是点电荷q 、A壳、B壳（带同样电荷时）单独存在时在A中形成的的电势的代数和，所以，当我们以球心O点为对象，有

U_O = k + k + k = 0

Q_B应指B球壳上的净电荷量，故 Q_B = 0

所以 Q_A = －q

☆学员讨论：A壳的各处电势均为零，我们的方程能不能针对A壳表面上的某点去列？（答：不能，非均匀带电球壳的球心以外的点不能应用定式！）

基于刚才的讨论，求B的电势时也只能求B的球心的电势（独立的B壳是等势体，球心电势即为所求）——

U_B = k + k

〖答〗（1）Q_A = －q ；（2）U_B = k(1－) 。

【物理情形2】图7-11中，三根实线表示三根首尾相连的等长绝缘细棒，每根棒上的电荷分布情况与绝缘棒都换成导体棒时完全相同。点A是Δabc的中心，点B则与A相对bc棒对称，且已测得它们的电势分别为U_A和U_B 。试问：若将ab棒取走，A、B两点的电势将变为多少？

【模型分析】由于细棒上的电荷分布既不均匀、三根细棒也没有构成环形，故前面的定式不能直接应用。若用元段分割→叠加，也具有相当的困难。所以这里介绍另一种求电势的方法。

每根细棒的电荷分布虽然复杂，但相对各自的中点必然是对称的，而且三根棒的总电量、分布情况彼此必然相同。这就意味着：①三棒对A点的电势贡献都相同（可设为U₁）；②ab棒、ac棒对B点的电势贡献相同（可设为U₂）；③bc棒对A、B两点的贡献相同（为U₁）。

所以，取走ab前  3U₁ = U_A

                 2U₂ + U₁ = U_B

取走ab后，因三棒是绝缘体，电荷分布不变，故电势贡献不变，所以

  U_A′= 2U₁

                 U_B′= U₁ + U₂

【答案】U_A′= U_A ；U_B′= U_A + U_B 。

〖模型变换〗正四面体盒子由彼此绝缘的四块导体板构成，各导体板带电且电势分别为U₁ 、U₂ 、U₃和U₄ ，则盒子中心点O的电势U等于多少？

〖解说〗此处的四块板子虽然位置相对O点具有对称性，但电量各不相同，因此对O点的电势贡献也不相同，所以应该想一点办法——

我们用“填补法”将电量不对称的情形加以改观：先将每一块导体板复制三块，作成一个正四面体盒子，然后将这四个盒子位置重合地放置——构成一个有四层壁的新盒子。在这个新盒子中，每个壁的电量将是完全相同的（为原来四块板的电量之和）、电势也完全相同（为U₁ + U₂ + U₃ + U₄），新盒子表面就构成了一个等势面、整个盒子也是一个等势体，故新盒子的中心电势为

U′= U₁ + U₂ + U₃ + U₄ 

最后回到原来的单层盒子，中心电势必为 U =  U′

〖答〗U = （U₁ + U₂ + U₃ + U₄）。

☆学员讨论：刚才的这种解题思想是否适用于“物理情形2”？（答：不行，因为三角形各边上电势虽然相等，但中点的电势和边上的并不相等。）

〖反馈练习〗电荷q均匀分布在半球面ACB上，球面半径为R ，CD为通过半球顶点C和球心O的轴线，如图7-12所示。P、Q为CD轴线上相对O点对称的两点，已知P点的电势为U_P ，试求Q点的电势U_Q 。

〖解说〗这又是一个填补法的应用。将半球面补成完整球面，并令右边内、外层均匀地带上电量为q的电荷，如图7-12所示。

从电量的角度看，右半球面可以看作不存在，故这时P、Q的电势不会有任何改变。

而换一个角度看，P、Q的电势可以看成是两者的叠加：①带电量为2q的完整球面；②带电量为－q的半球面。

考查P点，U_P = k + U_半球面

其中 U_半球面显然和为填补时Q点的电势大小相等、符号相反，即 U_半球面= －U_Q 

以上的两个关系已经足以解题了。

〖答〗U_Q = k － U_P 。

【物理情形3】如图7-13所示，A、B两点相距2L ，圆弧是以B为圆心、L为半径的半圆。A处放有电量为q的电荷，B处放有电量为－q的点电荷。试问：（1）将单位正电荷从O点沿移到D点，电场力对它做了多少功？（2）将单位负电荷从D点沿AB的延长线移到无穷远处去，电场力对它做多少功？

【模型分析】电势叠加和关系W_AB = q（U_A － U_B）= qU_AB的基本应用。

U_O = k + k = 0

U_D = k + k = －

U_∞ = 0

再用功与电势的关系即可。

【答案】（1）；（2）。 

【相关应用】在不计重力空间，有A、B两个带电小球，电量分别为q₁和q₂ ，质量分别为m₁和m₂ ，被固定在相距L的两点。试问：（1）若解除A球的固定，它能获得的最大动能是多少？（2）若同时解除两球的固定，它们各自的获得的最大动能是多少？（3）未解除固定时，这个系统的静电势能是多少？

【解说】第（1）问甚间；第（2）问在能量方面类比反冲装置的能量计算，另启用动量守恒关系；第（3）问是在前两问基础上得出的必然结论…（这里就回到了一个基本的观念斧正：势能是属于场和场中物体的系统，而非单纯属于场中物体——这在过去一直是被忽视的。在两个点电荷的环境中，我们通常说“两个点电荷的势能”是多少。）

【答】（1）k；（2）E_k1 = k ，E_k2 = k；（3）k 。

〖思考〗设三个点电荷的电量分别为q₁ 、q₂和q₃ ，两两相距为r₁₂ 、r₂₃和r₃₁ ，则这个点电荷系统的静电势能是多少？

〖解〗略。

〖答〗k（++）。

〖反馈应用〗如图7-14所示，三个带同种电荷的相同金属小球，每个球的质量均为m 、电量均为q ，用长度为L的三根绝缘轻绳连接着，系统放在光滑、绝缘的水平面上。现将其中的一根绳子剪断，三个球将开始运动起来，试求中间这个小球的最大速度。

〖解〗设剪断的是1、3之间的绳子，动力学分析易知，2球获得最大动能时，1、2之间的绳子与2、3之间的绳子刚好应该在一条直线上。而且由动量守恒知，三球不可能有沿绳子方向的速度。设2球的速度为v ，1球和3球的速度为v′，则

动量关系 mv + 2m v′= 0

能量关系 3k = 2 k + k + mv² + 2m

解以上两式即可的v值。

〖答〗v = q 。

三、电场中的导体和电介质

【物理情形】两块平行放置的很大的金属薄板A和B，面积都是S ，间距为d（d远小于金属板的线度），已知A板带净电量+Q₁ ，B板带尽电量+Q₂ ，且Q₂＜Q₁ ，试求：（1）两板内外表面的电量分别是多少；（2）空间各处的场强；（3）两板间的电势差。

【模型分析】由于静电感应，A、B两板的四个平面的电量将呈现一定规律的分布（金属板虽然很薄，但内部合场强为零的结论还是存在的）；这里应注意金属板“很大”的前提条件，它事实上是指物理无穷大，因此，可以应用无限大平板的场强定式。

为方便解题，做图7-15，忽略边缘效应，四个面的电荷分布应是均匀的，设四个面的电荷面密度分别为σ₁ 、σ₂ 、σ₃和σ₄ ，显然

（σ₁ + σ₂）S = Q₁ 

（σ₃ + σ₄）S = Q₂ 

A板内部空间场强为零，有 2πk（σ₁ ? σ₂ ? σ₃ ? σ₄）= 0

A板内部空间场强为零，有 2πk（σ₁ + σ₂ + σ₃ ? σ₄）= 0

解以上四式易得 σ₁ = σ₄ = 

               σ₂ = ?σ₃ = 

有了四个面的电荷密度，Ⅰ、Ⅱ、Ⅲ空间的场强就好求了〔如E_Ⅱ =2πk（σ₁ + σ₂ ? σ₃ ? σ₄）= 2πk〕。

最后，U_AB = E_Ⅱd

【答案】（1）A板外侧电量、A板内侧电量，B板内侧电量?、B板外侧电量；（2）A板外侧空间场强2πk，方向垂直A板向外，A、B板之间空间场强2πk，方向由A垂直指向B，B板外侧空间场强2πk，方向垂直B板向外；（3）A、B两板的电势差为2πkd，A板电势高。

〖学员思考〗如果两板带等量异号的净电荷，两板的外侧空间场强等于多少？（答：为零。）

〖学员讨论〗（原模型中）作为一个电容器，它的“电量”是多少（答：）？如果在板间充满相对介电常数为ε_r的电介质，是否会影响四个面的电荷分布（答：不会）？是否会影响三个空间的场强（答：只会影响Ⅱ空间的场强）？

〖学员讨论〗（原模型中）我们是否可以求出A、B两板之间的静电力？〔答：可以；以A为对象，外侧受力·（方向相左），内侧受力·（方向向右），它们合成即可，结论为F = Q₁Q₂ ，排斥力。〕

【模型变换】如图7-16所示，一平行板电容器，极板面积为S ，其上半部为真空，而下半部充满相对介电常数为ε_r的均匀电介质，当两极板分别带上+Q和?Q的电量后，试求：（1）板上自由电荷的分布；（2）两板之间的场强；（3）介质表面的极化电荷。

【解说】电介质的充入虽然不能改变内表面的电量总数，但由于改变了场强，故对电荷的分布情况肯定有影响。设真空部分电量为Q₁ ，介质部分电量为Q₂ ，显然有

Q₁ + Q₂ = Q

两板分别为等势体，将电容器看成上下两个电容器的并联，必有

U₁ = U₂ 即  =  ，即  = 

解以上两式即可得Q₁和Q₂ 。

场强可以根据E = 关系求解，比较常规（上下部分的场强相等）。

上下部分的电量是不等的，但场强居然相等，这怎么解释？从公式的角度看，E = 2πkσ（单面平板），当k 、σ同时改变，可以保持E不变，但这是一种结论所展示的表象。从内在的角度看，k的改变正是由于极化电荷的出现所致，也就是说，极化电荷的存在相当于在真空中形成了一个新的电场，正是这个电场与自由电荷（在真空中）形成的电场叠加成为E₂ ，所以

E₂ = 4πk（σ ? σ′）= 4πk（ ? ）

请注意：①这里的σ′和Q′是指极化电荷的面密度和总量；② E = 4πkσ的关系是由两个带电面叠加的合效果。

【答案】（1）真空部分的电量为Q ，介质部分的电量为Q ；（2）整个空间的场强均为 ；（3）Q 。

〖思考应用〗一个带电量为Q的金属小球，周围充满相对介电常数为ε_r的均匀电介质，试求与与导体表面接触的介质表面的极化电荷量。

〖解〗略。

〖答〗Q′= Q 。

四、电容器的相关计算

【物理情形1】由许多个电容为C的电容器组成一个如图7-17所示的多级网络，试问：（1）在最后一级的右边并联一个多大电容C′，可使整个网络的A、B两端电容也为C′？（2）不接C′，但无限地增加网络的级数，整个网络A、B两端的总电容是多少？

【模型分析】这是一个练习电容电路简化基本事例。

第（1）问中，未给出具体级数，一般结论应适用特殊情形：令级数为1 ，于是

 +  =  解C′即可。

第（2）问中，因为“无限”，所以“无限加一级后仍为无限”，不难得出方程

 +  = 

【答案】（1）C ；（2）C 。

【相关模型】在图7-18所示的电路中，已知C₁ = C₂ = C₃ = C₉ = 1μF ，C₄ = C₅ = C₆ = C₇ = 2μF ，C₈ = C₁₀ = 3μF ，试求A、B之间的等效电容。

【解说】对于既非串联也非并联的电路，需要用到一种“Δ→Y型变换”，参见图7-19，根据三个端点之间的电容等效，容易得出定式——

Δ→Y型：C_a = 

          C_b = 

          C_c = 

Y→Δ型：C₁ = 

         C₂ = 

         C₃ = 

有了这样的定式后，我们便可以进行如图7-20所示的四步电路简化（为了方便，电容不宜引进新的符号表达，而是直接将变换后的量值标示在图中）——

【答】约2.23μF 。

【物理情形2】如图7-21所示的电路中，三个电容器完全相同，电源电动势ε₁ = 3.0V ，ε₂ = 4.5V，开关K₁和K₂接通前电容器均未带电，试求K₁和K₂接通后三个电容器的电压U_ao 、U_bo和U_co各为多少。

【解说】这是一个考查电容器电路的基本习题，解题的关键是要抓与o相连的三块极板（俗称“孤岛”）的总电量为零。

电量关系：++= 0

电势关系：ε₁ = U_ao + U_ob = U_ao ? U_bo 

          ε₂ = U_bo + U_oc = U_bo ? U_co 

解以上三式即可。

【答】U_ao = 3.5V ，U_bo = 0.5V ，U_co = ?4.0V 。

【伸展应用】如图7-22所示，由n个单元组成的电容器网络，每一个单元由三个电容器连接而成，其中有两个的电容为3C ，另一个的电容为3C 。以a、b为网络的输入端，a′、b′为输出端，今在a、b间加一个恒定电压U ，而在a′b′间接一个电容为C的电容器，试求：（1）从第k单元输入端算起，后面所有电容器储存的总电能；（2）若把第一单元输出端与后面断开，再除去电源，并把它的输入端短路，则这个单元的三个电容器储存的总电能是多少？

【解说】这是一个结合网络计算和“孤岛现象”的典型事例。

（1）类似“物理情形1”的计算，可得 C_总 = C_k = C

所以，从输入端算起，第k单元后的电压的经验公式为 U_k = 

再算能量储存就不难了。

（2）断开前，可以算出第一单元的三个电容器、以及后面“系统”的电量分配如图7-23中的左图所示。这时，C₁的右板和C₂的左板（或C₂的下板和C₃的右板）形成“孤岛”。此后，电容器的相互充电过程（C₃类比为“电源”）满足——

电量关系：Q₁′= Q₃′

          Q₂′+ Q₃′= 

电势关系：+  = 

从以上三式解得 Q₁′= Q₃′=  ，Q₂′=  ，这样系统的储能就可以用得出了。

【答】（1）E_k = ；（2） 。

〖学员思考〗图7-23展示的过程中，始末状态的电容器储能是否一样？（答：不一样；在相互充电的过程中，导线消耗的焦耳热已不可忽略。）

☆第七部分完☆