
题目列表(包括答案和解析)
 (1)下列说法正确的是
(1)下列说法正确的是(1)(6分)下列说法正确的是(选对一个给2分,选对两个给4分,选对三个给6分,选错一个扣3分,最低得分为0分)
A.布朗运动虽然不是液体分子的运动,但是它可以说明分子在永不停息地做无规则运动
B.只要知道水的摩尔质量和一个水分子的质量,就可以计算出阿伏加德罗常数
C.在使两个分子间的距离由很远(r >10–9 m)减小到很难再靠近的过程中,分子间作用力先减小后增大,分子势能不断增大
D.通过科技创新,我们能够研制出内能全部转化为机械能的热机
E.内能不同的物体,它们分子热运动的平均动能可能相同
(2)(5分)在粗测油酸分子大小的实验中,具体操作如下:
①取纯油酸1.00mL注入容量为250mL的瓶内,然后向瓶中加入酒精,直到液面达到250mL的刻度为止,摇动瓶使油酸在酒精中充分溶解,形成油酸的酒精溶液;
②用滴管吸取制得的溶液逐滴滴入量筒,记录滴入的滴数直到量筒达到1.00mL为止,恰好共滴了100滴;
③在浅盘内注入约2cm深的水,将痱子粉均匀撒在水面上,再用滴管吸取油酸的酒精溶液,轻轻地向水面滴一滴溶液,油酸在水面上会很快散开,形成一油酸薄膜,待薄膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描出油酸薄膜的形状;
④将画有油酸薄膜轮廓形状的玻璃板,放在画有许多已知边长的小正方形的坐标纸上,计算出轮廓范围内正方形的总数,由小正方形边长和小正方形的总个数计算得此油膜面积为3.60×102cm2。
利用上述实验数据可求得油酸分子的直径为 m。(保留3位有效数字)
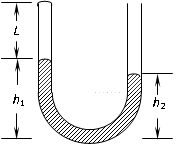
(3)(9分)如图所示,竖直放置的、左端封闭、右端开口的U形管中用水银柱封住一段空气柱L,当空气柱的温度为t1=7℃时,左臂水银柱的高度h1 =15cm,右臂水银柱的高度h2 = 10 cm,气柱长度L1=20cm;仅将管内被封住的空气柱加热到t2=127℃且稳定时,图中的h1变为h1′= 10cm。不考虑水银和管的热胀冷缩,大气压强始终不变。当时的大气压强多大?(单位用cmHg)

(1)(6分)下列说法正确的是(选对一个给2分,选对两个给4分,选对三个给6分,选错一个扣3分,最低得分为0分)
| A.布朗运动虽然不是液体分子的运动,但是它可以说明分子在永不停息地做无规则运动 |
| B.只要知道水的摩尔质量和一个水分子的质量,就可以计算出阿伏加德罗常数 |
| C.在使两个分子间的距离由很远(r >10–9 m)减小到很难再靠近的过程中,分子间作用力先减小后增大,分子势能不断增大 |
| D.通过科技创新,我们能够研制出内能全部转化为机械能的热机 |
| A.布朗运动虽然不是液体分子的运动,但是它可以说明分子在永不停息地做无规则运动 |
| B.只要知道水的摩尔质量和一个水分子的质量,就可以计算出阿伏加德罗常数 |
| C.在使两个分子间的距离由很远(r >10–9 m)减小到很难再靠近的过程中,分子间作用力先减小后增大,分子势能不断增大 |
| D.通过科技创新,我们能够研制出内能全部转化为机械能的热机 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com