
题目列表(包括答案和解析)

A.单缝S的作用是为了增加光的强度
B.双缝S1、S2的作用是为了产生两个频率相同的线状光源
C.当S1、S2发出的两列光的路程差为1.5λ时,产生第二暗纹(λ为光的波长)
D.当S1、S2发出的两列光的路程差为2λ时,产生第二明纹(λ为光的波长)
 λ=
λ=| 0.25×10-3×1.893×10-3 |
| 0.7 |
| d2 |
| L2 |
| d2 |
| L2 |
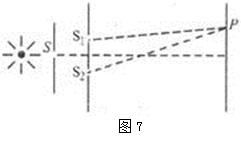
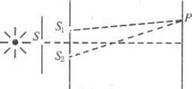
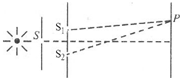 如图是单色光的双缝干涉的示意图,其中S为单缝、S1、S2为双缝,且三条缝互相平行,缝S到S1、S2的距离相等,下列说法中正确的是:( )
如图是单色光的双缝干涉的示意图,其中S为单缝、S1、S2为双缝,且三条缝互相平行,缝S到S1、S2的距离相等,下列说法中正确的是:( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com