
题目列表(包括答案和解析)
一圆锥透镜如图所示,
S、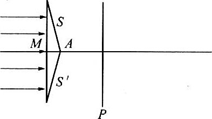
(1)用示意图画出在屏上看到的图像.当屏远移时图像怎样变化?
(2)设圆锥底面半径为R,锥面母线与底面的夹角为β(3°~5°).透镜材料的折射率为n.令屏离锥顶A的距离为x,求出为描述图像变化需给出的屏的几个特殊位置.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com