
题目列表(包括答案和解析)
匀速圆周运动、离心现象
1.匀速圆周运动:质点沿圆周运动,如果在相等的时间内通过的________相等,这种运动就叫做匀速成圆周运动.
2.向心力:做匀速圆周运动的物体所受到的始终指向圆心的合力,叫做向心力.向心力只能改变速度的________,不能改变速度的________.向心力的表达式为:________
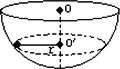
3.向心力始终沿半径指向圆心,________是分析向心力的关键,而圆周运动的圆心一定和物体做圆周运动的轨道在________.例如沿光滑半球内壁在水平面上做圆周运动的物体,匀速圆周运动的圆心在与小球同一水平面上的![]() 而不在球心O点(如图).
而不在球心O点(如图).
4.离心现象:做匀速圆周运动的物体,在合外力突然________,或者________物体做圆周运动所需要的向心力时,即:![]() .物体将做________,这种现象叫做离心现象.
.物体将做________,这种现象叫做离心现象.
描述圆周运动的物理量
1.线速度
①定义:质点做圆周运动通过的弧长S与通过这段弧长所用时间t的________叫做圆周运动的线速度.
②线速度的公式为________,
③方向为________.作匀速圆周运动的物体的速度、方向时刻在变化,因此匀速圆周运动是一种________运动.
2.角速度
①定义:用连接物体和圆心的半径转过的角度![]() 跟转过这个角度所用时间t的________叫做角速度.
跟转过这个角度所用时间t的________叫做角速度.
②公式为________,单位是________.
3.周期
①定义:做匀速圆周运动的物体运动________的时间,称为周期.
②公式:________
4.描述匀速圆周运动的各物理量的关系
①角速度ω与周期的关系是:________
②角速度和线速度的关系是:________
③周期与频率的关系是:________;
④向心加速度与以上各运动学物理量之间的关系:________
5.描述圆周运动的力学物理量是向心力(F向),它的作用是________.描述圆周运动的运动学物理量和力学物理量之间的关系是:________.
A.
| B.
| C.
| D.
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com