
题目列表(包括答案和解析)
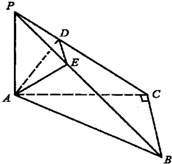 (理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.
(理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.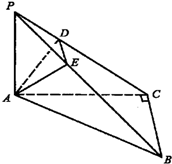 (理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.
(理)如图,P为△ABC所在平面外一点,且PA⊥平面ABC,∠ACB=90°,过点A作垂直于PC的截面ADE,截面交PC于点D,交PB于点E.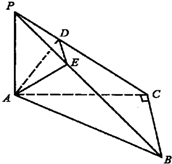
 为不等边△ABC所在平面外一点,O是P在△ABC内的射影,且O在△ABC内部。有下列条件:
为不等边△ABC所在平面外一点,O是P在△ABC内的射影,且O在△ABC内部。有下列条件:
⑴ PA、PB、PC两两垂直; ⑵ 点P到△ABC三边的距离相等;
⑶ PA⊥BC,PB⊥AC; ⑷ PA、PB、PC与平面ABC所成的角相等;
⑸ 平面PBC、PAB、PAC与平面ABC所成的角相等; ⑹ PA=PB=PC;
⑺ ∠PAB=∠PAC,∠PBA=∠PBC,∠PCB=∠PCA.
若从上述7个条件中任意取出两个(只取一次)作为条件,一个必能得出O为△ABC的内心,另一个必能得出O为△ABC的外心的取法有___________种.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com