
题目列表(包括答案和解析)
 (2009•江苏一模)已知如图所示的矩形,长为12,宽为5,在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆数为600颗,则可以估计出阴影部分的面积约为
(2009•江苏一模)已知如图所示的矩形,长为12,宽为5,在矩形内随机地投掷1000颗黄豆,数得落在阴影部分的黄豆数为600颗,则可以估计出阴影部分的面积约为(2009江苏卷)在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为 . ![]()
(2009江苏卷)在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为 .
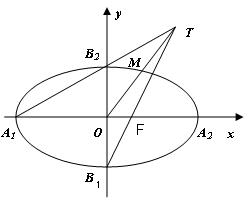
(2009江苏卷)如图,在平面直角坐标系![]() 中,
中,![]() 为椭圆
为椭圆![]() 的四个顶点,
的四个顶点,![]() 为其右焦点,直线
为其右焦点,直线![]() 与直线
与直线![]() 相交于点T,线段
相交于点T,线段![]() 与椭圆的交点
与椭圆的交点![]() 恰为线段
恰为线段![]() 的中点,则该椭圆的离心率为 .
的中点,则该椭圆的离心率为 .
(2009江苏卷)设![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]() ,令
,令![]() ,若数列
,若数列![]() 有连续四项在集合
有连续四项在集合![]() 中,则
中,则![]() = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com