题目列表(包括答案和解析)
如图，F为抛物线
的焦点，A、B、C为该抛物线上三点，若
，则
等于
A．6 B．4
C．3 D．2
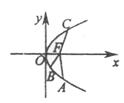
如图，F是抛物线
的焦点，Q是准线与x轴的交点，直线
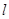经过点Q。
（Ⅰ）直线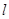与抛物线有唯一公共点，求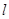方程；
（Ⅱ）直线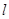与抛物线交于A、B两点；
（i）设FA、FB的斜率分别为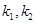
，求
的值；
（ii）若点R在线段AB上，且满足
，求点R的轨迹方程。
的焦点，Q是准线与x轴的交点，直线
经过点Q。与抛物线有唯一公共点，求方程；与抛物线交于A、B两点；
，求
的值；
，求点R的轨迹方程。
如图，F为抛物线y2＝4x的焦点，A、B、C在抛物线上，若
＋
＋
＝
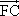，则||＋||＋|
|＝
6
4
3
2
如图，F为抛物线y2＝4x的焦点，A、B、C在抛物线上，若
，则
6
4
3
2
一、选择题
1. B 2. C 3. A 4. D 5. C 6. D 7. B 8. C 9. A 10. D
二、填空题
11. 192 12. 286 13. 
14. 
15.
840 16. 
三、解答题
17. （本题12分）
解：（I）
2分
（II）
8分
由已知条件
根据正弦定理，得
10分
12分
18. （本题12分）
解：（I）在7人中选出3人，总的结果数是
种， （2分）
记“被选中的3人中至多有1名女生”为事件A，则A包含两种情形：
①被选中的是1名女生，2名男生的结果数是
，
②被选中的是3名男生的结果数是
4分
至多选中1名女生的概率为
6分
（II）由题意知随机变量
可能的取值为：0，1，2，3，则有
，
8分
∴
0
1
2
3
P
10分
∴的数学期望
12分
19. （本题12分）
解：（I）连接PO，以OA，OB，OP所在的直线为x轴，y轴，z轴
建立如图所示的空间直角坐标系。 2分
∵正四棱锥的底面边长和侧棱长都是2。
∴
∴
（II）∵
∴
是平面PDB的一个法向量。 8分
由（I）得
设平面BMP的一个法向量为
则由
，得
，不妨设c=1
得平面BMP的一个法向量为
10分
∵二面角M―PB―D小于90°
∴二面角M―PB―D的余弦值为
12分
20. （本题12分）
解：（I）由已知得
2分
由
，得 4分
即
。解得k=50或
（舍去）
6分
（II）由
，得
8分
9分
是等差数列
则
11分
12分
21. （本题14分）
解：（I）依题意得
2分
把
解得
∴椭圆的方程为
4分
（II）由（I）得
，设
，如图所示，
∵M点在椭圆上，
∴
①
∵M点异于顶点A、B，
∴
由P、A、M三点共线，可得
，
从而
7分
∴
② 8分
将①式代入②式化简得
10分
∵
∴
12分
于是∠MBP为锐角，从而∠MBN为钝角，
∴点B在以MN为直径的圆内。 14分
22. （本题14分）
解：（I）
，
令
2分
而
∴当
4分
（II）设函数g(x)在[0，2]上的值域是A，
∵若对任意
∴
6分
①当
，
∴函数
上单调递减。
∵
∴
； 8分
②当
令
（舍去） 9分
（i）当
时，
的变化如下表：
（ii）当
∴函数g(x)在（0，2）上单调递减。
综上可知，实数a的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com