
题目列表(包括答案和解析)
已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。第一问,利用函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中设切点为(x0,x03-3x0),因为过点A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分离参数∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函数求导数,判定单调性,从而得到要是有三解,则需要满足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依题意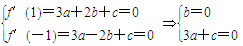
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)设切点为(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0)
又切线过点A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
令g(x)=-2x3+6x2-6
则g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
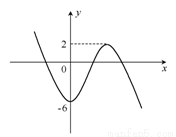
∴g(x)在(-∞,0)单调递减,(0,2)单调递增,(2,+∞)单调递减.
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当-6<m<2时,m=-2x3+6x2-6有三解,
所以m的取值范围是(-6,2).
已知函数 ,
, .
.
(Ⅰ)若函数 依次在
依次在 处取到极值.求
处取到极值.求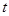 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的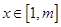 ,不等式
,不等式
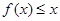 恒成立.求正整数
恒成立.求正整数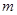 的最大值.
的最大值.
【解析】第一问中利用导数在在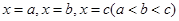 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的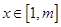 ,不等式
,不等式
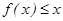 恒成立转化为
恒成立转化为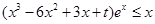 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式 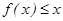 ,即
,即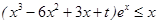 ,即
,即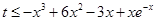 .
.
转化为存在实数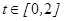 ,使对任意的
,使对任意的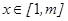 ,不等式
,不等式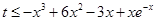 恒成立.
恒成立.
即不等式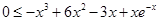 在
在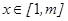 上恒成立.
上恒成立.
即不等式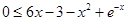 在
在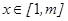 上恒成立.
上恒成立.
设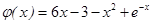 ,则.
,则.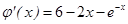
设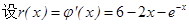 ,则
,则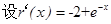 ,因为
,因为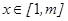 ,有
,有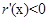 .
.
故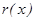 在区间
在区间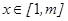 上是减函数。又
上是减函数。又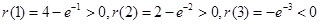
故存在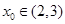 ,使得
,使得 .
.
当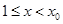 时,有
时,有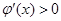 ,当
,当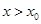 时,有
时,有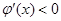 .
.
从而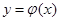 在区间
在区间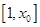 上递增,在区间
上递增,在区间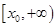 上递减.
上递减.
又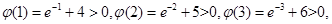 [来源:]
[来源:]
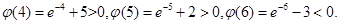
所以当 时,恒有
时,恒有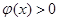 ;当
;当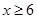 时,恒有
时,恒有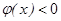
 ;
;
故使命题成立的正整数m的最大值为5
甲船由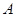 岛出发向北偏东
岛出发向北偏东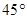 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为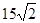 海里∕小时,在甲船从
海里∕小时,在甲船从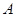 岛出发的同时,乙船从
岛出发的同时,乙船从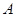 岛正南
岛正南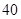 海里处的
海里处的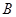 岛出发,朝北偏东
岛出发,朝北偏东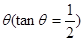 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为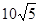 海里∕小时。
海里∕小时。
⑴求出发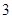 小时时两船相距多少海里?
小时时两船相距多少海里?
⑴ 两船出发后多长时间相距最近?最近距离为多少海里?
【解析】第一问中根据时间得到出发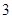 小时时两船相距的海里为
小时时两船相距的海里为
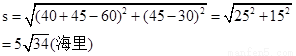
第二问设时间为t,则
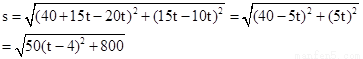
利用二次函数求得最值,
解:⑴依题意有:两船相距
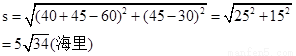
答:出发3小时时两船相距 海里
海里
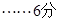
⑵两船出发后t小时时相距最近,即
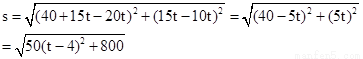
即当t=4时两船最近,最近距离为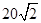 海里。
海里。
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)证明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
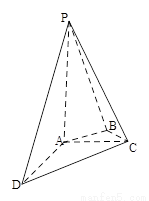
【解析】解法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0), 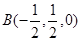 ,P(0,0,2).
,P(0,0,2).
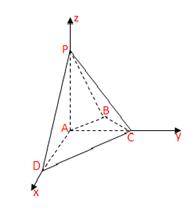
(1)证明:易得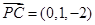 ,
,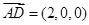 于是
于是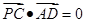 ,所以
,所以
(2) 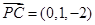 ,
,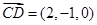 设平面PCD的法向量
设平面PCD的法向量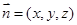 ,
,
则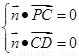 ,即
,即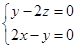 .不防设
.不防设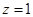 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量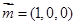 于是
于是 从而
从而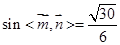 .
.
所以二面角A-PC-D的正弦值为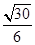 .
.
(3)设点E的坐标为(0,0,h),其中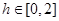 ,由此得
,由此得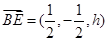 .
.
由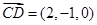 ,故
,故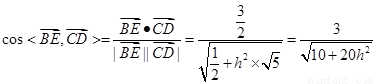
所以, ,解得
,解得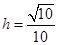 ,即
,即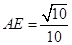 .
.
解法二:(1)证明:由 ,可得
,可得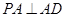 ,又由
,又由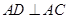 ,
,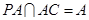 ,故
,故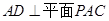 .又
.又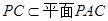 ,所以
,所以 .
.

(2)如图,作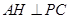 于点H,连接DH.由
于点H,连接DH.由 ,
,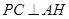 ,可得
,可得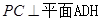 .
.
因此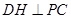 ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在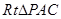 中,
中,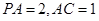 ,由此得
,由此得 由(1)知
由(1)知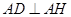 ,故在
,故在 中,
中,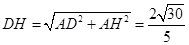
因此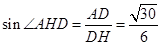 所以二面角
所以二面角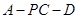 的正弦值为
的正弦值为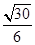 .
.
(3)如图,因为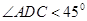 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故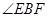 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故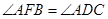 .在
.在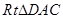 中,
中, 故
故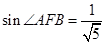
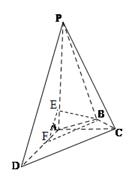
在 中,由
中,由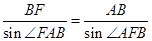 ,
,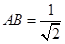 ,
,
可得 .由余弦定理,
.由余弦定理,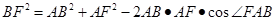 ,
,
所以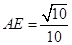 .
.
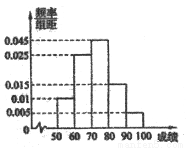
山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
【解析】本试题主要考查了概率的运算和统计图的运用。
(1)由由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05,然后利用平均值公式,可知这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)
(2)中利用90~100分数段的人数为2人,频率为0.05;得到总参赛人数为40,然后得到0~60分数段的人数为40×0.1=4人,第五组中有2人,这样可以得到基本事件空间为15种,然后利用其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种,得到概率值
解:(Ⅰ)由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05; ……………2分
∴这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)…4分
(Ⅱ)∵90~100分数段的人数为2人,频率为0.05;
∴参加测试的总人数为 =40人,……………………………………5分
=40人,……………………………………5分
∴50~60分数段的人数为40×0.1=4人, …………………………6分
设第一组50~60分数段的同学为A1,A2,A3,A4;第五组90~100分数段的同学为B1,B2
则从中选出两人的选法有:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种;其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种 …………………………11分
则选出的两人为“帮扶组”的概率为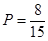
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com