
题目列表(包括答案和解析)
.定义在R上的函数f(x)满足f(4)=1,f′(x)为函数f(x)的导函数.已知函数y=f′(x)的图象如图2所示,两个正数a、b满足f(2a+b)<1,则![]() 的取值范围是( )
的取值范围是( )

图2
A.(![]() ,
,![]() ) B.(-∞,
) B.(-∞,![]() )∪(3,+∞) C.(
)∪(3,+∞) C.(![]() ,3) D.(-∞,-3)
,3) D.(-∞,-3)
(1)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(2)对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;
(3)在AB上是否存在两个不同的点D′,E′,使沿折线.PD′E′O修建公路的总造价小于(2)中得到的最小总造价?证明你的结论.
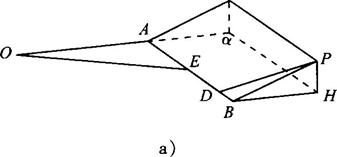
a)
第19题图
(文)如图b所示,直四棱柱ABCD-A1B1C1D1中,∠ADC=90°,△ABC为等边三角形,且AA1=AD=DC=2.
(1)求AC1与BC所成角的余弦值;
(2)求二面角C1-BD-C的大小;
(3)设M是BD上的点,当DM为何值时,D1M⊥平面A1C1D?并证明你的结论.
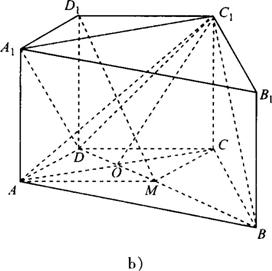
第19题图
(1)求曲线C的方程;
(2)已知点A(5,0)、B(1,0),过点A作直线交曲线C于两个不同的点P、Q,△BPQ的面积S是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
(文)如图b所示,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A,B到x轴距离之积为2m,以x轴为对称轴、过A,O,B三点作抛物线.
(1)求抛物线方程;
(2)若tan∠AOB=-1,求m的取值范围.
第21题图
三个12cm×12cm的正方形纸片都被连接两条邻边的中点的直线分成两片,如图a所示,把所得的六片纸片粘在一个正六边形的外面,如图b所示,然后折成多面体,如图c所示,则此多面体的体积是
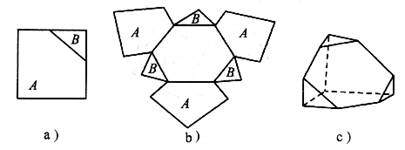
A.216cm3 B.648cm3 C.864cm3 D.1728cm3
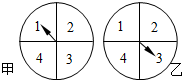 同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=4的概率为( )
同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=4的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com