题目列表(包括答案和解析)
已知：抛物线y＝x2－(2m＋4)x＋m2－10与x轴交于A、B两点，C是抛物线的顶点．
(1)用配方法求顶点C的坐标(用含m的代数式表示)；
(2)“若AB的长为2
，求抛物线的解析式．”解法的部分步骤如下，补全解题过程，并简述步骤①的解题依据，步骤②的解题方法．
解：由(1)知，对称轴与x轴交于点D( ，0)．
∵抛物线的对称性及AB＝2
，
∴AD＝BD＝|xA－xD|＝
．
∵点A(xA，0)在抛物线y＝(x－h)2＋k上，
∴0＝(xA－h)2＋k． ①
∵h＝xC＝xD，将|xA－xD|＝
代入上式，得到关于m的方程
0＝(
)2＋( ) ②
(3)将(2)中的条件“AB的长为2
”改为“△ABC为等边三角形”，用类似的方法求出此抛物线的解析式．
已知抛物线y＝x2－(2m＋4)x＋m2－10与x轴交于A、B两点，C是抛物线的顶点．
(1)用配方法求顶点C的坐标(用含有m的代数式表示)；
(2)“若AB的长为2
，求抛物线的解析式”的解法如下：
由(1)知，对称轴与x轴交于点D(________，0)．
∵抛物线具有对称性，且AB＝2
，
∴AD＝DB＝|xA－xD|＝．
∵A(xA，0)在抛物线y＝(x－h)2＋k上，
∴(xA－h)2＋k＝0． ①
∵h＝xC＝xD，
∴将|xA－xD|＝
代入①，得到关于m的方程0＝(
)2＋(________)． ②
补全解题过程，并简述步骤①的解题依据，步骤②的解题方法．
(3)将(2)中条件“AB的长为2
”改为“△ABC为等边三角形”，用类似的方法求出抛物线的解析式．
已知抛物线y＝x2－2x＋a(a＜0)与y轴相交于点A，顶点为M．直线
分别与x轴，y轴相交于B，C两点，并且与直线AM相交于点N．
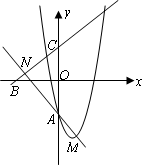
(1)填空：试用含a的代数式分别表示点M与N的坐标，则M( ， )，N( ， )；
(2)如下图，将△NAC沿y轴翻折，若点N的对应点
恰好落在抛物线上，
与x轴交于点D，连结CD，求a的值和四边形ADCN的面积；
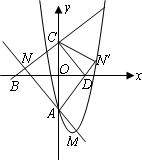
(3)在抛物线y＝x2－2x＋a(a＜0)上是否存在一点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出P点的坐标；若不存在，试说明理由．
如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以毎秒1个单位长的速度运动t秒(t＞0)，抛物线y＝x2＋bx＋c经过点O和点P，已知矩形ABCD的三个顶点为A(1，0)，B(1，－5)，D(4，0)．
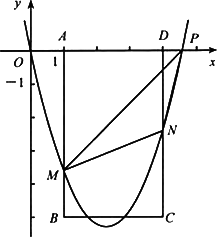
(1)求c，b(用含t的代数式表示)：
(2)当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．
①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；
②求△MPN的面积S与t的函数关系式，并求t为何值时，S＝
；
(3)在矩形ABCD的内部(不含边界)，把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围．
如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以毎秒1个单位长的速度运动t秒(t＞0)，抛物线y＝x2＋bx＋c经过点O和点P，已知矩形ABCD的三个顶点为A(1，0)，B(1，－5)，D(4，0)．
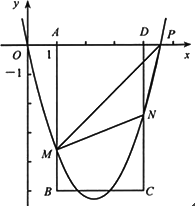
(1)求c，b(用含t的代数式表示)：
(2)当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．
①在点P的运动过程中，你认为cos∠AMP的大小是否会变化？若变化，说明理由；若不变，求出cos∠AMP的值；
②求△MPN的面积S与t的函数关系式，并求t为何值时，
；
(3)在矩形ABCD的内部(不含边界)，把横、纵坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围是________．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com