
题目列表(包括答案和解析)
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数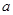 使得数列
使得数列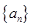 满足:若
满足:若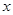 是数列
是数列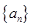 中的一项,则
中的一项,则 也是数列
也是数列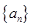 中的一项,称数列
中的一项,称数列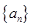 为“兑换数列”,常数
为“兑换数列”,常数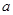 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: 是“兑换系数”为
是“兑换系数”为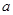 的“兑换数列”,求
的“兑换数列”,求 和
和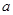 的值;
的值;
(2)已知有穷等差数列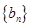 的项数是
的项数是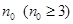 ,所有项之和是
,所有项之和是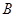 ,求证:数列
,求证:数列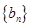 是“兑换数列”,并用
是“兑换数列”,并用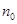 和
和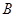 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列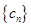 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
 使得数列
使得数列 满足:若
满足:若 是数列
是数列 中的一项,则
中的一项,则 也是数列
也是数列 中的一项,称数列
中的一项,称数列 为“兑换数列”,常数
为“兑换数列”,常数 是它的“兑换系数”.
是它的“兑换系数”. 是“兑换系数”为
是“兑换系数”为 的“兑换数列”,求
的“兑换数列”,求 和
和 的值;
的值; 的项数是
的项数是 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列 是“兑换数列”,并用
是“兑换数列”,并用 和
和 表示它的“兑换系数”;
表示它的“兑换系数”; ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
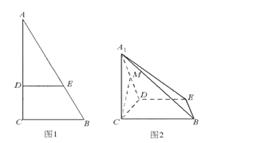
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1) 求证:A1C⊥平面BCDE;
(2) 若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3) 线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由
【解析】(1)∵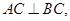 DE∥BC∴
DE∥BC∴ ∴
∴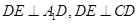 ∴
∴ ∴
∴ 又∵
又∵ ∴
∴
(2)如图,以C为坐标原点,建立空间直角坐标系C-xyz,
则
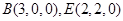
设平面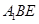 的法向量为
的法向量为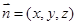 ,则
,则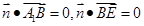 ,又
,又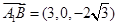 ,
,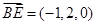 ,所以
,所以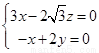 ,令
,令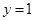 ,则
,则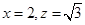 ,所以
,所以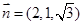 ,
,
设CM与平面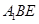 所成角为
所成角为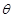 。因为
。因为 ,
,
所以
所以CM与平面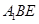 所成角为
所成角为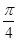 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com