
题目列表(包括答案和解析)
定义两种运算:a![]() b=
b=![]() ,a
,a![]() b=
b=![]() ,则函数f(x)=
,则函数f(x)=![]() 的解析式为
的解析式为
A.f(x)=![]() ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
B.f(x)=![]() ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)
C.f(x)=![]() ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)
D.f(x)=![]() ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
定义两种运算:a⊕b=![]() ,a⊗b=
,a⊗b=![]() ,则函数f(x)=
,则函数f(x)=![]() 的解析式为
的解析式为
( )
A.f(x)=![]() ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
B.f(x)=![]() ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)
C.f(x)=-![]() ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)
D.f(x)=-![]() ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
对于两种运算:a?b= ,a⊗b=
,a⊗b= ,则函数f(x)=
,则函数f(x)=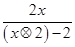 的解析式为( )
的解析式为( )
A.f(x)= ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
B.f(x)= ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)
C.f(x)=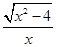 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)
D.f(x)= ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
 ,a?b=
,a?b= ,则函数f(x)=
,则函数f(x)= 的解析式为( )
的解析式为( )A.f(x)= ,x∈[-2,0)∪(0,2] ,x∈[-2,0)∪(0,2] |
B.f(x)= ,x∈(-∞,-2]∪[2,+∞) ,x∈(-∞,-2]∪[2,+∞) |
C.f(x)= ,x∈(-∞,-2]∪[2,+∞) ,x∈(-∞,-2]∪[2,+∞) |
D.f(x)= ,x∈[-2,0)∪(0,2] ,x∈[-2,0)∪(0,2] |
已知点P在曲线C:y=![]() (x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
(x>1)上,设曲线C在点P处的切线为l,若l与函数y=kx(k>0)的图像交于点A,与x轴交于点B,设点P的横坐标为t,设A、B的横坐标分别为xA、xB,记f(t)=xA·xB.
(Ⅰ)求f(t)的解析式;
(Ⅱ)设数列{an}(n≥1,n∈N)满足a1=1,an=f(![]() )(n≥2),数列{bn}(n≥1,n∈N)满足bn=
)(n≥2),数列{bn}(n≥1,n∈N)满足bn=![]() ,求{an}和{bn}的通项公式;
,求{an}和{bn}的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当1<k<3时,证明不等式:a1+a2+a3+…+an>![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com