
题目列表(包括答案和解析)
三、解答题 :(本大题共5小题,每小题12分,共60分。解答应写出证明过程或演算步骤)
19.(本小题满分12分)
对某校110个小学生进行心理障碍测试得到如下的列联表:
|
|
焦虑 |
说谎 |
懒惰 |
总计 |
|
女生 |
5 |
10 |
15 |
30 |
|
男生 |
20 |
10 |
50 |
80 |
|
总计 |
25 |
20 |
65 |
110 |
通过计算说明在这三种心理障碍中哪一种与性别关系最大?
三、解答题(本大题有5道小题,各小题12分,共60分)
17.在 中,
中, 分别是角
分别是角 的对边,向量
的对边,向量 ,
, ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在
在
区间 上的最大值和最小值.
上的最大值和最小值.
(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—5:不等式选讲
设函数 .
.
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若不等式 的解集是非空的集合,求实数
的解集是非空的集合,求实数 的取值范围.
的取值范围.
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本小题满分14分) A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆O与轴正半轴的交点, 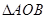 为等腰直角三角形。记
为等腰直角三角形。记 (1)若A点的坐标为
(1)若A点的坐标为 ,求
,求
 的值 (2)求
的值 (2)求 的取值范围。
的取值范围。
 |
某人从2010年9月1日起,每年这一天到银行存款一年定期1万元,且每年到期的存款将本和利再存入新一年的一年定期,若一年定期存款利率![]() 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】
A. 11314元 B. 53877元 C. 11597元 D.63877元
三、解答题(本题满分85分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对
应的题号)内写出必要的步骤.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com