
题目列表(包括答案和解析)
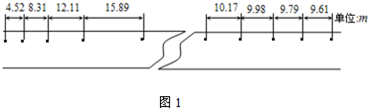
| s | 2 |
| s | 2 |
| πd2R |
| 4l |
| πd2R |
| 4l |
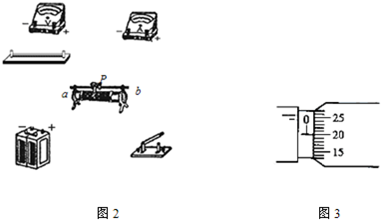

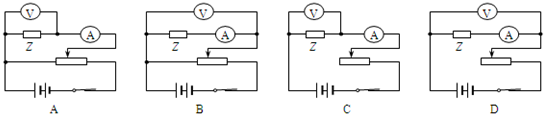
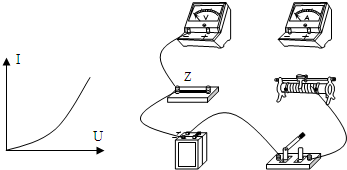
| 2gL(1-cosα) |
| 2gL(1-cosα) |
|
|
| 2gL(1-cosα) |
|
| 2gL(1-cosβ) |
| 2gL(1-cosα) |
|
| 2gL(1-cosβ) |
(20分)一对正、负电子可形成一种寿命比较短的称为电子偶素的新粒子.电子偶素中的正电子与负电子都以速率v绕它们连线的中点做圆周运动.假定玻尔关于氢原子的理论可用于电子偶素,电子的质量m、速率v和正、负电子间的距离r的乘积也满足量子化条件.即![]() 式中n称为量子数,可取整数值1,2,3,…;h为普朗克常量.试求电子偶素处在各定态时的r和能量以及第一激发态与基态能量之差.
式中n称为量子数,可取整数值1,2,3,…;h为普朗克常量.试求电子偶素处在各定态时的r和能量以及第一激发态与基态能量之差.
(20分)薄膜材料气密性能的优劣常用其透气系数来加以评判.对于均匀薄膜材料,在一定温度下,某种气体通过薄膜渗透过的气体分子数![]() ,其中t为渗透持续时间,S为薄膜的面积,d为薄膜的厚度,
,其中t为渗透持续时间,S为薄膜的面积,d为薄膜的厚度,![]() 为薄膜两侧气体的压强差.k称为该薄膜材料在该温度下对该气体的透气系数.透气系数愈小,材料的气密性能愈好.
为薄膜两侧气体的压强差.k称为该薄膜材料在该温度下对该气体的透气系数.透气系数愈小,材料的气密性能愈好.

图为测定薄膜材料对空气的透气系数的一种实验装置示意图.EFGI为渗透室,U形管左管上端与渗透室相通,右管上端封闭;U形管内横截面积A=0.150cm2.实验中,首先测得薄膜的厚度d =0.66mm,再将薄膜固定于图中![]() 处,从而把渗透室分为上下两部分,上面部分的容积
处,从而把渗透室分为上下两部分,上面部分的容积![]() ,下面部分连同U形管左管水面以上部分的总容积为V1,薄膜能够透气的面积S =1.00cm2.打开开关K1、K2与大气相通,大气的压强P1=1.00atm,此时U形管右管中气柱长度
,下面部分连同U形管左管水面以上部分的总容积为V1,薄膜能够透气的面积S =1.00cm2.打开开关K1、K2与大气相通,大气的压强P1=1.00atm,此时U形管右管中气柱长度![]() ,
,![]() .关闭K1、K2后,打开开关K3,对渗透室上部分迅速充气至气体压强
.关闭K1、K2后,打开开关K3,对渗透室上部分迅速充气至气体压强![]() ,关闭K3并开始计时.两小时后, U形管左管中的水面高度下降了
,关闭K3并开始计时.两小时后, U形管左管中的水面高度下降了![]() .实验过程中,始终保持温度为
.实验过程中,始终保持温度为![]() .求该薄膜材料在
.求该薄膜材料在![]() 时对空气的透气系数.(本实验中由于薄膜两侧的压强差在实验过程中不能保持恒定,在压强差变化不太大的情况下,可用计时开始时的压强差和计时结束时的压强差的平均值
时对空气的透气系数.(本实验中由于薄膜两侧的压强差在实验过程中不能保持恒定,在压强差变化不太大的情况下,可用计时开始时的压强差和计时结束时的压强差的平均值![]() 来代替公式中的
来代替公式中的![]() .普适气体常量R = 8.31Jmol-1K-1,1.00atm = 1.013×105Pa).
.普适气体常量R = 8.31Jmol-1K-1,1.00atm = 1.013×105Pa).
(20分)如图所示,接地的空心导体球壳内半径为R,在空腔内一直径上的P1和P2处,放置电量分别为q1和q2的点电荷,q1=q2=q,两点电荷到球心的距离均为a.由静电感应与静电屏蔽可知:导体空腔内表面将出现感应电荷分布,感应电荷电量等于-2q.空腔内部的电场是由q1、q2和两者在空腔内表面上的感应电荷共同产生的.由于我们尚不知道这些感应电荷是怎样分布的,所以很难用场强叠加原理直接求得腔内的电势或场强.但理论上可以证明,感应电荷对腔内电场的贡献,可用假想的位于腔外的(等效)点电荷来代替(在本题中假想(等效)点电荷应为两个),只要假想的(等效)点电荷的位置和电量能满足这样的条件,即:设想将整个导体壳去掉,由q1在原空腔内表面的感应电荷的假想(等效)点电荷![]() 与q1共同产生的电场在原空腔内表面所在位置处各点的电势皆为0;由q2在原空腔内表面的感应电荷的假想(等效)点电荷
与q1共同产生的电场在原空腔内表面所在位置处各点的电势皆为0;由q2在原空腔内表面的感应电荷的假想(等效)点电荷![]() 与q2共同产生的电场在原空腔内表面所在位置处各点的电势皆为0.这样确定的假想电荷叫做感应电荷的等效电荷,而且这样确定的等效电荷是唯一的.等效电荷取代感应电荷后,可用等效电荷
与q2共同产生的电场在原空腔内表面所在位置处各点的电势皆为0.这样确定的假想电荷叫做感应电荷的等效电荷,而且这样确定的等效电荷是唯一的.等效电荷取代感应电荷后,可用等效电荷![]() 、
、![]() 和q1、q2来计算原来导体存在时空腔内部任意点的电势或场强。
和q1、q2来计算原来导体存在时空腔内部任意点的电势或场强。

1.试根据上述条件,确定假想等效电荷![]() 、
、![]() 的位置及电量.
的位置及电量.
2.求空腔内部任意点A的电势UA.已知A点到球心O的距离为r,![]() 与
与![]() 的夹角为q .
的夹角为q .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com