练习册

  • 练习册
  • 试题
    (二)解答题: 2.用数学归纳法证明:当时., (II)对于.已知. 求证:., (III)求出满足等式的所有正整数. 解法1:(Ⅰ)证:用数学归纳法证明: (ⅰ)当时.原不等式成立,当时.左边.右边. 因为.所以左边右边.原不等式成立, (ⅱ)假设当时.不等式成立.即.则当时. ..于是在不等式两边同乘以得 . 所以．即当时.不等式也成立． 综合知.对一切正整数.不等式都成立． (Ⅱ)证:当时.由(Ⅰ)得. 于是.． 知.当时. . ． 即．即当时.不存在满足该等式的正整数． 故只需要讨论的情形: 当时..等式不成立, 当时..等式成立, 当时..等式成立, 当时.为偶数.而为奇数.故.等式不成立, 当时.同的情形可分析出.等式不成立． 综上.所求的只有． 解法2:(Ⅰ)证:当或时.原不等式中等号显然成立.下用数学归纳法证明: 当.且时..． ① (ⅰ)当时.左边.右边.因为.所以.即左边右边.不等式①成立, (ⅱ)假设当时.不等式①成立.即.则当时. 因为.所以．又因为.所以． 于是在不等式两边同乘以得 . 所以．即当时.不等式①也成立． 综上所述.所证不等式成立． (Ⅱ)证:当.时... 而由(Ⅰ).. ． (Ⅲ)解:假设存在正整数使等式成立. 即有． ② 又由(Ⅱ)可得 .与②式矛盾． 故当时.不存在满足该等式的正整数． 下同解法1． 3.已知函数.且存在.使. (I)证明:是上的单调增函数,(II)设. 其中.证明:,(III)证明:. 解: (I)∵f '(x)=3x2-2x+ = 3(x-)2+ >0 . ∴f(x)是R上的单调增函数． (II)∵0<x0< . 即x1<x0<y1．又f(x)是增函数. ∴f(x1)<f(x0)<f(y1)．即x2<x0<y2． 又x2=f(x1)=f(0)=>0 =x1. y2=f(y1)=f()=<=y1.综上. x1<x2<x0<y2<y1． 用数学归纳法证明如下: (1)当n=1时.上面已证明成立． (2)假设当n=k(k≥1)时有xk<xk+1<x0<yk+1<yk ． 当n=k+1时.由f(x)是单调增函数.有f(xk)<f(xk+1)<f(x0)<f(yk+1)<f(yk).∴xk+1<xk+2<x0<yk+2<yk+1 由知对一切n=1.2.-.都有xn<xn+1<x0<yn+1<yn． (III) = = yn2+xnyn+xn2-(yn+xn)+ ≤(yn+xn)2-(yn+xn)+ =[(yn+xn)-]2+ ． 由(Ⅱ)知 0<yn+xn<1．∴- < yn+xn- < . ∴ < ()2+ = 4.已知数列满足:.且 (1)求数列的通项公式, (2)证明:对于一切正整数.不等式. 解: (1) 将条件变为:1-＝.因此{1-}为一个等比数列.其首项为 1-＝.公比.从而1-＝.据此得an＝----1° (2) 证:据1°得.a1·a2·-an＝ 为证a1·a2·--an<2·n! 只要证nÎN*时有>----2° 显然.左端每个因式都是正数.先证明.对每个nÎN*.有 ³1-()----3° 用数学归纳法证明3°式: (i) n＝1时.3°式显然成立. (ii) 设n＝k时.3°式成立. 即³1-() 则当n＝k+1时. ³(1-())·() ＝1-()-+() ³1-(+)即当n＝k+1时.3°式也成立. 故对一切nÎN*.3°式都成立. 利用3°得.³1-()＝1- ＝1-> 故2°式成立.从而结论成立. 【查看更多】

     

    题目列表(包括答案和解析)

    二、解答题：本大题共6小题，共90分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤。
    15、（本小题满分14分）在△ABC中，角A、B、C所对应的边为
    （1）若 求A的值；
    （2）若，求的值.

    查看答案和解析>>

     

    三、解答题：解答应写出文字说明、证明过程或演算步骤（本大题共6个大题，共76分）。

    17．（12分）以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系：

    销售经验（年）

    1

    3

    4

    4

    6

    8

    10

    10

    11

    13

    年销售额（千元）

    80

    97

    92

    102

    103

    111

    119

    123

    117

    136

     （1）依据这些数据画出散点图并作直线＝78＋4．2x，计算（yi－i）2； 

     （2）依据这些数据由最小二乘法求线性回归方程，并据此计算；

     （3）比较（1）和（2）中的残差平方和的大小．

     

    查看答案和解析>>

    某公司招聘员工采取两次考试(笔试)的方法：第一试考选择题，共10道题（均为四选一题型），每题10分，共100分；第二试考解答题，共3题。规则是：只有在一试中达到或超过80分者才获通过并有资格参加二试，参加二试的人只有答对2题或3题才能被录用。现有甲、乙两人参加该公司的招聘考试。且已知在一试时：两人均会做10道题中的6道；对于另外4道题来说，甲有两题可排除两个错误答案、有两题完全要猜，乙有两题可排除一个错误答案、有一题可排除两个错误答案、有一题完全要猜。进入二试后，对于任意一题，甲答对的概率是、乙答对的概率是.（1）分别求甲、乙两人能通过一试进入二试的概率、；（2）求甲、乙两人都能被录用的概率.

     

    查看答案和解析>>

    三、解答题：本大题共5小题，共72分。解答应写出文字说明、证明过程或演算步骤。

     

    18.（本小题满分14分） A、B是单位圆O上的动点，且A、B分别在第一、二象限，C是圆O与轴正半轴的交点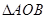， 为等腰直角三角形。记 (1)若A点的坐标为，求 的值    (2)求的取值范围。

     

     

     

     

     

     

     

    查看答案和解析>>

    小明的父亲下岗后，打算利用自己的技术特长和本地资源开一间副食品加工厂，经测算，当日产量在100千克至250千克时，日生产总成本y(元)可近似地看成日产量x(千克)的二次函数，当日产量为100千克时，日总成本为2000元，当日产量为150千克时，日总成本最低，为1750元，又知产品现在的售价为每千克16元．

    (1)把日生产总成本y(元)写成日产量x(千克)的函数；

    (2)将y÷x称为平均成本，问日产量为多少千克时，平均成本最低？

    (3)当日产量为多大时，才能保证加工厂不亏本？

    (结果要求精确到个位，参考数值：≈1.1，≈3.6)

    查看答案和解析>>


    同步练习册答案