
题目列表(包括答案和解析)
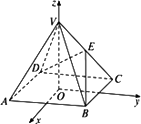
如图所示,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC的中点,正四棱锥底面边长为2a,高为h.求线段BE的长.
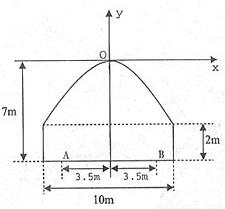
 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米. 以O为原点,
以O为原点,| OA |
| OA |
| AG |
| OG |
 以O为原点,
以O为原点, 所在直线为x轴,建立如图所示的直角坐标系.若
所在直线为x轴,建立如图所示的直角坐标系.若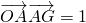 ,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).
,点A的坐标为(t,0),t∈(0,+∞),点G的坐标为(m,3).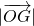 取最小值时双曲线C的方程;
取最小值时双曲线C的方程;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com