.files/image174.jpg)
解法二:取SB、BC的中点分别为G、H,
连结AG、GB、AH、由CH//SC,AB//DC,
得面AGB//面SDC。
∴所求的二面角即为面AGH与面AGB所成的角
由于AG⊥SB,BR⊥面SAB。
∴∠BGH为所求二面角的平面角。
在直角三角GBD中,.files/image178.gif) ,
,
即面SDC与面SAB所成二面角的正切值为.files/image180.gif) …………13分
…………13分
18.解:(1)某员工获得一等奖的概率为.files/image182.gif) ………………4分
………………4分
(2)∵某员工获三等奖的概率为.files/image184.gif) …………………7分
…………………7分
获二等奖的概率为.files/image186.gif) …………………9分
…………………9分
∴某员工所获奖品价值Y(无)的概率分布为:
Y
200
100
50
P
.files/image188.gif)
.files/image190.gif)
.files/image192.gif)
……………………10分
(3)EY=200×.files/image188.gif) +100×
+100×.files/image190.gif) +50×
+50×.files/image192.gif) =
=.files/image194.gif)
∴该单位需准备奖品的价值约为.files/image196.gif) 元………………13分
元………………13分
19.解:.files/image198.gif) …………2分
…………2分
(1).files/image200.gif)
∴曲线.files/image202.gif) 处的切线方程为
处的切线方程为.files/image204.gif)
即.files/image206.gif) ………………4分
………………4分
(2)令.files/image208.gif)
当.files/image210.gif)
令.files/image212.gif)
.files/image214.gif) 上为减函数,在
上为减函数,在.files/image216.gif) 上增函数。…………6分
上增函数。…………6分
当.files/image218.gif) 在R上恒成立。
在R上恒成立。
.files/image220.gif) 上为减函数。……………………7分
上为减函数。……………………7分
当.files/image222.gif)
令.files/image224.gif)
.files/image226.gif)
在.files/image228.gif) 上为增函数。…………………………8分
上为增函数。…………………………8分
综上,当.files/image230.gif) 时,
时,.files/image232.gif)
单调递减区间为.files/image234.gif) 。
。
当.files/image236.gif)
当.files/image238.gif)
单调递减区间为(.files/image240.gif) ),(
),(.files/image242.gif) )……………………9分
)……………………9分
(3)a>0时,列表得:
.files/image244.gif)
.files/image246.gif)
.files/image248.gif)
.files/image216.gif)
1
(1,+.files/image251.gif) )
)
.files/image253.gif)
+
0
-
0
+
.files/image119.gif)
ㄊ
极大值
ㄋ
极小值
ㄊ
又.files/image255.gif)
从而,当.files/image257.gif) …………11分
…………11分
由题意,不等式.files/image121.gif) 恒成立,
恒成立,
所以得.files/image260.gif)
从而a的取值范围为.files/image262.gif) ……………………13分
……………………13分
20.解:(Ⅰ)圆.files/image264.gif) ,
,
半径.files/image266.gif)
.files/image268.gif)
.files/image270.gif) QM是P的中垂线,连结AQ,则|AQ|=|QP|
QM是P的中垂线,连结AQ,则|AQ|=|QP|
.files/image272.gif)
又.files/image274.gif) ,
,
根据椭圆的定义,点Q轨迹是以C(-.files/image276.gif) ,0),A(
,0),A(.files/image276.gif) ,0)为焦点,长轴长为2
,0)为焦点,长轴长为2.files/image278.gif) 的椭圆,……………………2分
的椭圆,……………………2分
由.files/image280.gif) 因此点Q的轨迹方程为
因此点Q的轨迹方程为.files/image282.gif) ………………4分
………………4分
(Ⅱ)(1)证明:当直线l垂直x轴时,由题意知:.files/image284.gif)
不妨取.files/image286.gif) 代入曲线E的方程得:
代入曲线E的方程得:
.files/image288.gif)
即G(.files/image290.gif) ,
,.files/image290.gif) ),H(
),H(.files/image290.gif) ,-
,-.files/image290.gif) )有两个不同的交点,………………5分
)有两个不同的交点,………………5分
当直线l不垂直x轴时,设直线l的方程为:.files/image292.gif)
由题意知:.files/image294.gif)
由.files/image296.gif)
.files/image298.gif)
∴直线l与椭圆E交于两点
综上,直线l必与椭圆E交于两点…………………………8分
(2)由(1)知当直线l垂直x轴时,.files/image300.gif)
.files/image302.gif) ………………9分
………………9分
当直线l不垂直x轴时
设.files/image304.gif) (1)知
(1)知
.files/image306.gif)
.files/image308.gif)
.files/image310.gif)
.files/image312.gif)
.files/image314.gif) …………………………10分
…………………………10分
.files/image316.gif)
当且仅当.files/image318.gif) ,则取得“=”
,则取得“=”
.files/image320.gif) ……………………12分
……………………12分
当k=0时,.files/image322.gif) …………………………13分
…………………………13分
综上,△OGH的面积的最小值为.files/image324.gif) ……………………14分
……………………14分
21.(1)解:矩阵A的特征多项式为
.files/image326.gif) …………………………2分
…………………………2分
令.files/image328.gif) ,得矩阵A的特征值为
,得矩阵A的特征值为.files/image330.gif) ……………………………3分
……………………………3分
对于特征值.files/image332.gif) 解相应的线性方程组
解相应的线性方程组.files/image334.gif) 得一个非零解
得一个非零解.files/image336.gif) ,
,
因此,.files/image338.gif) 是矩阵A的属于特征值
是矩阵A的属于特征值.files/image340.gif) 的一个特征向量。…………5分
的一个特征向量。…………5分
对于特征值.files/image342.gif) 解相应的线性方程组
解相应的线性方程组.files/image344.gif) 得一个非零解
得一个非零解.files/image346.gif) ,
,
因此,.files/image348.gif) 是矩阵A的属于特征值
是矩阵A的属于特征值.files/image350.gif) 的一个特征向量。………………7分
的一个特征向量。………………7分
2.解:(1)两圆的极坐标方程可化为.files/image352.gif)
∴两圆的直角坐标方程是.files/image354.gif) ………………4分
………………4分
(2)根据(1)可知道两圆心的直角坐标是O1(1,0)和O2(0,a)
.files/image356.gif) ……………………7分
……………………7分
3.解:(1)∵.files/image358.gif)
∴当x<1时,3-2x>3,解得x<0;
当1.files/image360.gif) 无解
无解
当x>2时2x-3>3,解得x<3.
综上,x<0或x>3,
∴不等式f(x)>3的解集为.files/image362.gif) ……………………4分
……………………4分
(2)∵.files/image364.gif) ∴
∴.files/image366.gif)
∵.files/image368.gif) 恒成立
恒成立
∴a<1,即实数a的取值范围是.files/image370.gif) ………………………………7分
………………………………7分

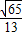
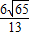


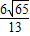


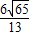
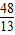


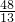
.files/image143.gif) 12.甲 13.7 14.
12.甲 13.7 14..files/image145.gif) 15.①③⑤
15.①③⑤.files/image147.gif) ……………………………………………………2分
……………………………………………………2分.files/image149.gif) ………………………………………………………………4分
………………………………………………………………4分.files/image151.gif)
.files/image153.gif)
.files/image155.gif) ………………………………………………………………6分
………………………………………………………………6分.files/image157.gif) ………………………………………………9分
………………………………………………9分.files/image159.gif) …………………………11分
…………………………11分.files/image161.gif) ………………………………………………13分
………………………………………………13分