练习册

  • 练习册
  • 试题
    6．解:(I)由 -2分 当 故 所以上为减函数.----4分 上为减函数. 由则: -6分 在上恒成立.即上恒成立, 即 由基本不等式得:----8分 (II)证明:因为上为减函数. 又 即①----11分 又当上为减函数. 即② 由①②可得得证.----15分 7(台州市2008学年第一学期高三年级期末质量评估试题 数 学(文))22．已知定义在上的函数.其中为常数. (1)若.求证:函数在区间上是增函数, (2)若函数.在处取得最大值.求正数的取值范围. 【查看更多】

     

    题目列表(包括答案和解析)

    给出问题：已知满足，试判定的形状.某学生的解答如下：

    解：（i）由余弦定理可得，

    ，

    ，

    ,

    故是直角三角形.

    （ii）设外接圆半径为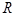.由正弦定理可得，原式等价于

    ，

    故是等腰三角形.

    综上可知，是等腰直角三角形.

    请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果.　　    　　　　　.

     

    查看答案和解析>>


    同步练习册答案