
题目列表(包括答案和解析)
(本小题满分14分)
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为![]() ,两镇的中心
,两镇的中心![]() 相距8个单位距离,环形高速公路所在的曲线为
相距8个单位距离,环形高速公路所在的曲线为![]() ,且
,且![]() 上的点到
上的点到![]() 的距离之和为10个单位距离,在曲线
的距离之和为10个单位距离,在曲线![]() 上建一个加油站
上建一个加油站![]() 与一个收费站
与一个收费站![]() ,使
,使![]() 三点在一条直线上,并且
三点在一条直线上,并且![]() 个单位距离.
个单位距离.
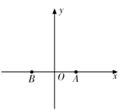 (1) 建立如图的直角坐标系,求曲线
(1) 建立如图的直角坐标系,求曲线![]() 的方程及
的方程及![]() 之间的距离有多少个单位距离;
之间的距离有多少个单位距离;
(2) ![]() 之间有一条笔直公路
之间有一条笔直公路![]() 与X轴正方向成
与X轴正方向成![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,该县招商部门引进外资在四边形
两点,该县招商部门引进外资在四边形![]() 区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
(本小题满分14分) 如图:在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图1),图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.
|

|
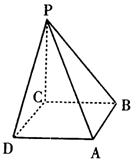
(1)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积.
(2)图3中,L、E均为棱PB上的点,且![]() ,
,![]() ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.

(本小题满分14分)
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.
(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值。

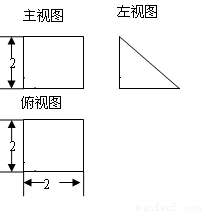
.(本小题满分14分)三棱柱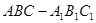 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,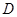 为
为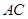 的中点.
的中点.
(1)求证: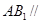 平面
平面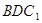 ;
;
(2)求证: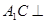 平面
平面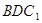 ;
;
(3)求二面角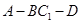 的正切值.
的正切值.
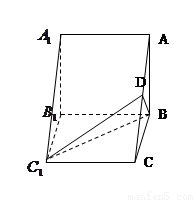
(本小题满分14分)
如图,平行四边形 中,
中,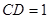 ,
, ,且
,且 ,正方形
,正方形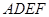 所在平面和平面
所在平面和平面 垂直,
垂直, 分别是
分别是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥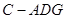 的体积.
的体积.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com