
题目列表(包括答案和解析)
| |||||||||||
| |||||||||||||||
| |||||||||||||||
设椭圆 (常数
(常数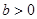 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一问中解:设 ,
, 则
则
由 得
得 由
由 ,得
,得
 ②
②

第二问易求椭圆 的标准方程为:
的标准方程为:
 ,
,
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .
.
解:设 ,
, ……………………1分
……………………1分
则 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求椭圆 的标准方程为:
的标准方程为: .………………2分
.………………2分
 , ……4分
, ……4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值
解答题:解答应写出文字说明,证明过程或演算步骤.
已知函数f(x)=mx3-3(m+1)x2+3(m+2)x+1,其中m∈R.
(Ⅰ)若m<0,求f(x)的单调区间;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-1,1]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围;
(Ⅲ)设g(x)=mx3-(3m+2)x2+3mx+4lnx+m+1,问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com