
题目列表(包括答案和解析)
如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
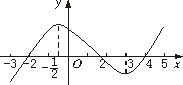
(1)函数y=f(x)在区间(-3,-![]() )内单调递增;
)内单调递增;
(2)函数y=f(x)在区间(-![]() ,3)内单调递减;
,3)内单调递减;
(3)函数y=f(x)在区间(4,5)内单调递增;
(4)当x=2时,函数y=f(x)有极小值;
(5)当x=-![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是________.
如果函数y=f(x-1)与y=f-1(x-1)的图象关于直线y=x对称,,那么![]() 等于
等于
f(x-1)
B.-f(x-1)
f(x-1)-1
f(x-1)+1
已知函数y=f(x)在区间[a,b]上均有意义,且A、B是其图象上横坐标分别为a、b的两点.对应于区间[0,1]内的实数λ,取函数y=f(x)的图象上横坐标为x=λa+(1-λ)b的点M,和坐标平面上满足![]() =λ
=λ![]() +(1-λ)
+(1-λ)![]() 的点N,得
的点N,得![]() .对于实数k,如果不等式|
.对于实数k,如果不等式|![]() |≤k对λ∈[0,1]恒成立,那么就称函数f(x)在[a,b]上“k阶线性近似”.若函数y=x2+x在[1,2]上“k阶线性近似”,则实数k的取值范围为
|≤k对λ∈[0,1]恒成立,那么就称函数f(x)在[a,b]上“k阶线性近似”.若函数y=x2+x在[1,2]上“k阶线性近似”,则实数k的取值范围为
![]()
B.[0,+∞)
C.[![]() ,+∞)
,+∞)
D.[![]() ,+∞)
,+∞)
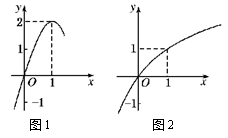
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
⑴分别求出函数f(x)和g(x)的解析式;
⑵如果函数y=g(f(x))在区间[1,m)上单调递减,求m的取值范围.

 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
⑴分别求出函数f(x)和g(x)的解析式;
⑵如果函数y=g(f(x))在区间[1,m)上单调递减,求m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com