
题目列表(包括答案和解析)
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
解::因为![]() ,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=
,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=![]() 与y=-
与y=-![]() 在(0,+
在(0,+![]() )上都是增函数,因此
)上都是增函数,因此![]() 在(0,+
在(0,+![]() )上是增函数,所以零点个数只有一个方法2:把函数
)上是增函数,所以零点个数只有一个方法2:把函数![]() 的零点个数个数问题转化为判断方程
的零点个数个数问题转化为判断方程![]() 解的个数问题,近而转化成判断
解的个数问题,近而转化成判断![]() 与
与![]() 交点个数问题,在坐标系中画出图形
交点个数问题,在坐标系中画出图形
由图看出显然一个交点,因此函数![]() 的零点个数只有一个
的零点个数只有一个
袋中有50个大小相同的号牌,其中标着0号的有5个,标着n号的有n个(n=1,2,…9),现从袋中任取一球,求所取号码的分布列,以及取得号码为偶数的概率.
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
某地区的羊患某种病的概率是0.4,且每只羊患病与否是彼此独立的,今研制一种新的预防药,任选6只羊做实验,结果6只羊服用此药后均未患病. 你认为这种药是否有效?
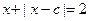 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com