练习册

  • 练习册
  • 试题
    11．如下图所示.在△ABC中.AB＝AC.AD是边BC的中线.P为AD上一点.CF∥AB.BP的延长线分别交AC.CF于点E.F.求证:BP2＝PE·PF. [分析] 要证明BP2＝PE·PF可以考虑将这三条线段组成两个相似三角形.这两个相似三角形应分别有一条边等于BP.考虑求证中涉及线段的位置关系.可取与BP相等的线段PC. [证明] 连结PC.∵AB＝AC.∴中线AD是此等腰三角形的对称轴． ∴∠ABP＝∠ACP.PB＝PC.又∵CF∥AB. ∴∠CFP＝∠ABP＝∠PCE. 又∵∠CPF为两个三角形的公共角. ∴△CPE∽△FPC. ∴＝. ∴BP2＝PC2＝PE·PF. 【查看更多】

     

    题目列表(包括答案和解析)

    如下图所示，某校把一块边长为2a的等边△ABC的边角地辟为生物园，图中DE把生物园分成面积相等的两部分，D在AB上，E在AC上．

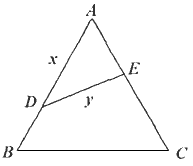
    (1)设AD＝x(x≥a)，ED＝y，求用x表示y的函数关系式；

    (2)如果DE是灌溉水管的位置，为了省钱，希望它最短，DE的位置应该在哪里？如果DE是参观线路，即希望它最长，DE的位置又应该在哪里？请给予证明．

    查看答案和解析>>

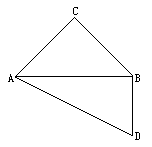
    将一副三角板放在同一个平面上组成下图所示的四边形ACBD，△ABC中，∠C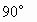＝，AC＝BC，△ABD中，∠AB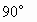D＝，∠D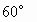＝．设AC＝a．现将四边形ACBD沿着AB翻折成直二面角C－AB－D，连结CD得一个四面体(如下图)．

    　　

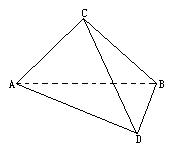
    (1)求证：平面ACD⊥平面BCD；

    (2)求直线AD和BC所成的角；

    (3)求直线AD和平面BCD所成的角；

    (4)求平面ACD和平面ABD所成二面角的大小．

    查看答案和解析>>


    同步练习册答案