
题目列表(包括答案和解析)
对对数函数的图象和性质的研究,教材是根据互为反函数的图象特征,由指数函数的图象再作出其关于直线y=x的图象,即得对数函数的图象,在数形结合的数学思想指导下,推得对数函数的性质.请归纳对数函数y=logax(a>0且a≠1)的性质.
在函数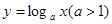 的图象上有
的图象上有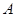 、
、 、
、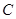 三点,横坐标分别为
三点,横坐标分别为 其中
其中 .
.
⑴求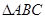 的面积
的面积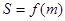 的表达式;
的表达式;
⑵求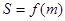 的值域.
的值域.
【解析】由题意利用分割可先表示三角形ABC的面积,然后应用对数运算性质及二次函数的性质求解函数的最大值,属于知识的简单综合.
| 1-sinx |
| 1+sinx |
| 性质 | 理由 | 结论 | 得分 |
| 定义域 | |||
| 值域 | |||
| 奇偶性 | |||
| 周期性 | |||
| 单调性 | | ||
| 对称性 | |||
| 作图 |
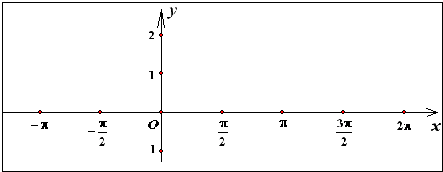 |
||
已知函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.
(Ⅰ)已知函数 ,
, ,判断
,判断 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(Ⅱ)已知函数 若
若 具有性质
具有性质 ,求
,求 的最大值;
的最大值;
(Ⅲ)若函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足 ,
,
求证:对任意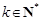 且
且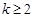 ,函数
,函数 具有性质
具有性质 .
.
已知函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.
(Ⅰ)已知函数 ,
, ,判断
,判断 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(Ⅱ)已知函数 若
若 具有性质
具有性质 ,求
,求 的最大值;
的最大值;
(Ⅲ)若函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足 ,
,
求证:对任意 且
且 ,函数
,函数 具有性质
具有性质 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com