
题目列表(包括答案和解析)
. (本小题满分12分)2009年4月22日是第40个“世界地球日” (World Earth Day),在某校举办的《2009“世界地球日”》知识竞赛中,甲、乙、丙三人同时回答一道有关保护地球知识的问题,已知甲回答对这道题的概率是![]() ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是![]() ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是![]() .
.
(Ⅰ)求乙、丙两人各自回答对这道题的概率.
(Ⅱ)求甲、乙、丙三人中恰有两人回答对该题的概率.
(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中![]() 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有![]() 持金卡,在省内游客中有
持金卡,在省内游客中有![]() 持银卡。
持银卡。
(Ⅰ)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(Ⅱ)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率。
(2009湖南卷理)(本小题满分12分)
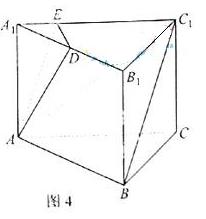
如图4,在正三棱柱![]() 中,
中,![]()
D是![]() 的中点,点E在
的中点,点E在![]() 上,且
上,且![]() 。
。
(I) 证明平面![]() 平面
平面![]()
(II) 求直线![]() 和平面
和平面![]() 所成角的正弦值。
所成角的正弦值。 ![]()
![]()
(2009辽宁卷理)(本小题满分12分)
某人向一目射击4次,每次击中目标的概率为![]() 。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设X表示目标被击中的次数,求X的分布列;
(Ⅱ)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A) ![]()
![]()
(2009湖南卷理)(本小题满分12分)w.w.w.k.s.5.u.c.o.m ![]()
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的.![]() 、
、![]() 、
、![]() ,现在3名工人独立地从中任选一个项目参与建设。
,现在3名工人独立地从中任选一个项目参与建设。 ![]()
![]()
(I)求他们选择的项目所属类别互不相同的概率;
(II)记![]() 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求
为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求![]() 的分布列及数学期望。
的分布列及数学期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com