
题目列表(包括答案和解析)
(本题满分14分)为赢得2010年上海世博会的制高点,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值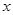 (单位:万元,
(单位:万元,
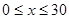 )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成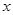 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
( (本题满分14分)为赢得2010年广州亚运会的商机,某商家最近进行了新科技产品的市场分析,调查显示,新产品每件成本9万元,售价为30万元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值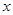 (单位:万元,
(单位:万元,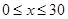 )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.(1)将一个星期的商品销售利润表示成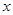 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
(本小题满分14分)
某公司计划2010年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过180000元,甲、乙两个电视台的广告收费标准分别为 元/分钟和
元/分钟和 元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为3000元和2000元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少元?
元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为3000元和2000元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少元?
(本题满分14分)
随着国家政策对节能环保型小排量车的调整,两款 升排量的Q型车、R型车的销量引起市场的关注。已知2010年1月Q型车的销量为
升排量的Q型车、R型车的销量引起市场的关注。已知2010年1月Q型车的销量为 辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式:
辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式: .
.
(1)求Q型车前n个月的销售总量Sn的表达式;
(2)比较两款车前n个月的销售总量Sn与Tn的大小关系;
(3)试问从第几个月开始Q型车的月销售量小于R型车月销售量的20%,并说明理由.
(参考数据
 )
)
(本题满分14分)
随着国家政策对节能环保型小排量车的调整,两款 升排量的Q型车、R型车的销量引起市场的关注。已知2010年1月Q型车的销量为
升排量的Q型车、R型车的销量引起市场的关注。已知2010年1月Q型车的销量为 辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式:
辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式: .
.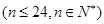
(1)求Q型车前n个月的销售总量Sn的表达式;
(2)比较两款车前n个月的销售总量Sn与Tn的大小关系;
(3)试问从第几个月开始Q型车的月销售量小于R型车月销售量的20%,并说明理由.
(参考数据
 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com