
题目列表(包括答案和解析)
(2010.十堰)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
(2010.十堰)如图所示,直线AB与反比例函数图像相交于A,B两点,已知A(1,4).
(1)求反比例函数的解析式;
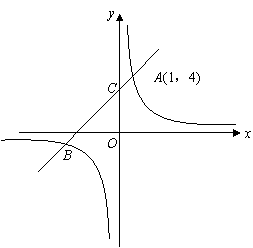
(2)连结OA,OB,当△AOB的面积为![]() 时,求直线AB的解析式.
时,求直线AB的解析式.
(2010.十堰)如图所示,某地区对某种药品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x + 70,y2=2x-38,需求量为0时,即停止供应.当y1=y2时,该药品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该药品的稳定价格与稳定需求量.
(2)价格在什么范围内,该药品的需求量低于供应量?
(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加6万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.

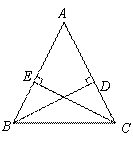
(2010.十堰)如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.
求证:BD=CE.
(2010.十堰)暑假快到了,老家在十堰的大学生张明与王艳打算留在上海,为世博会做义工.学校争取到6个义工名额,分别安排在中国馆园区3个名额,世博轴园区2个名额,演义中心园区1个名额. 学校把分别标号为1、2、3、4、5、6的六个质地大小均相同的小球,放在不透明的袋子里,并规定标号1、2、3的到中国馆,标号4、5到世博轴,标号6的到演艺中心,让张明、王艳各摸1个.
(1)求张明到中国馆做义工的概率;
(2)求张明、王艳各自在世博轴、演艺中心做义工的概率(两人不同在一个园区内).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com