（1）子集的定义：对于两个集合A和B，如果集合A的任意一个元素都是集合B的元素，我们就说集合A　　　　　集合B，或集合B　　　　　集合A，也可以说集合A是集合B的子集.记作　　　　　或　　　　　，如果集合A不包含于集合B，或集合B不包含集合A，就记作　　　　　.?

规定：空集是任何集合的子集, .?

如果AB，并且A≠B,称集合A是集合B的，记作　　　　　.?

（2）交集的定义：一般地，由属于集合A　　　　　属于集合B的元素所组成的集合，叫做A、B的交集.记作　　　　　（读作“A交B”），即A∩B=｛x|x∈A且x∈B｝.?

（3）并集的定义：一般地，由属于集合A　　　　　属于集合B的元素所组成的集合，叫做A、B的并集.记作　　　　　（读作“A并B”），即A∪B={x|x∈A或x∈B}).?

（4）补集的定义：一般地，设S是一个集合，A是S的一个子集，由S中所有　　　　　A的元素组成的集合，叫做S中子集A的补集（或余集），记作　　　　　，.?

 

(1)列举法：把集合中的元素　　　　　出来，写在　　　　　内表示集合的方法.列举法表示集合的特点是清晰、直观.集合中元素的个数较少时常适用于列举法.?

(2)描述法：把集合中的元素　　　　　的描述出来，写在　　　　　内表示集合的方法.一般形式是{x|p}，其中竖线前面的x叫做此集合的代表元素，竖线后面的p指出元素x所具有的公共属性.描述法便于从整体上把握一个集合，常适用于集合中元素的公共属性较为明显时.

(3)韦恩图：为了形象地表示集合，有时常用一些封闭的　　　　　表示一个集合，这样的图形称为韦恩图，在解题时，利用韦恩图“数”和“形”结合，使得解答十分直观.?

如集合A={a，b，c}可形象地表示为图(1)或图(2).?

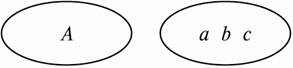
                        (1)　　　　            　　(2)

给出四个命题，其中正确命题的个数是(　)

　　(1)直线a⊥平面a ，直线b∥平面a ，则a⊥b；

　　(2)空间一个角的两边与另一个角的两边垂直，则这两个角互补；

　　(3)直线a平面a ，直线b平面a ，若a∥a ，b∥a ，则a∥b；

　　(4)一条直线垂直于一个平面内的无数条直线，则这条直线垂直于这个平面．

　　A．4个　　　　 B．3个　　　　 C．2个　　　　 D．1个

给出四个命题，其中正确命题的个数是(　)

　　(1)直线a⊥平面a ，直线b∥平面a ，则a⊥b；

　　(2)空间一个角的两边与另一个角的两边垂直，则这两个角互补；

　　(3)直线a平面a ，直线b平面a ，若a∥a ，b∥a ，则a∥b；

　　(4)一条直线垂直于一个平面内的无数条直线，则这条直线垂直于这个平面．

　　A．4个　　　　 B．3个　　　　 C．2个　　　　 D．1个

(1)一条直线和一个平面平行，它就和这个平面内的任何直线平行．

(　　)

(2)如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直．

(　　)

(3)垂直于三角形两边的直线必垂直于第三边．

(　　)

(4)过点A垂直于直线a的所有直线都在过点A垂直于a的平面内．

(　　)

(5)如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面．

(　　)