
题目列表(包括答案和解析)
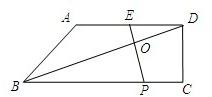 已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.(10分)已知:如图,在梯形ABCD中,AD∥BC,∠DCB = 90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为![]() ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
①当![]() = 1时,是 ;
= 1时,是 ;
②当![]() = 2时,是 ;
= 2时,是 ;
③当![]() = 3时,是 .
= 3时,是 .
请证明![]() = 2时的结论.
= 2时的结论.
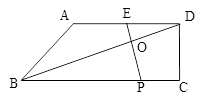

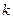 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?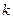 = 1时,是 ;
= 1时,是 ;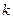 = 2时,是 ;
= 2时,是 ;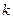 = 3时,是 .
= 3时,是 .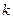 = 2时的结论.
= 2时的结论.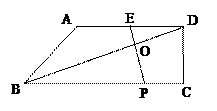


 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当 = 1时,是 ;②当
= 1时,是 ;②当 = 2时,是 ;③当
= 2时,是 ;③当 = 3时,是 . 并证明
= 3时,是 . 并证明 = 2时的结论.
= 2时的结论.(9分)已知:如图,在梯形ABCD中,AD∥BC,∠DCB = 90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.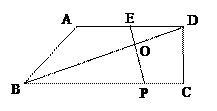
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为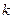 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当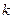 = 1时,是 ;②当
= 1时,是 ;②当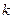 = 2时,是 ;③当
= 2时,是 ;③当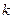 = 3时,是 . 并证明
= 3时,是 . 并证明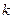 = 2时的结论.
= 2时的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com