题目列表(包括答案和解析)
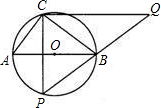半径为2.5的⊙O中，直径AB的不同侧有定点C和动点P．已知BC：CA=4：3，点P在 |
| AB |
|
| AB |
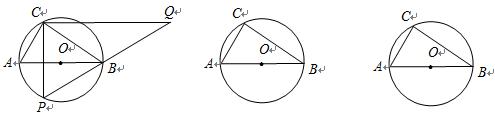
半径为5的⊙O中，直径AB的不同侧有定点C和动点P. 已知BC∶CA=4∶3，点P在弧AB上运动，过点C作CP的垂线，与PB的延长线交于点Q．
【小题1】 求证：△ABC∽△PQC；
【小题2】 当点P与点C关于AB对称时，求CQ的长；
【小题3】 当点P运动到什么位置时，CQ取到最大值？求此时CQ的长；
【小题4】当点P运动到弧AB的中点时，求CQ的长．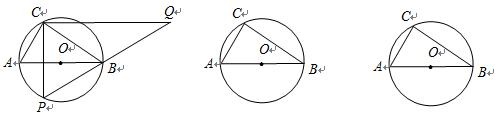
半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，⊙O与l相切于点F，DC在l上．
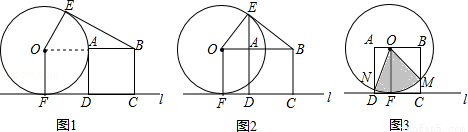
（1）过点B作的一条切线BE，E为切点．
①填空：如图1，当点A在⊙O上时，∠EBA的度数是 ；
②如图2，当E，A，D三点在同一直线上时，求线段OA的长；
（2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围．
一、选择题（本题共10小题，每小题4分，共40分）
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
A
A
D
B
A
C
B
二、填空题（本题共6小题，每小题5分，共30分）
11．
12．
13．
14．
15．
16．
三、解答题（本题有8小题，共80分）
17．（本题8分）
（1）原式
（2）解：
得：
，
，
把代入①得：
，
18．（本题8分）
（1）证明：
，
，
在
和
中
（2）答案不惟一，如：
，
，
等．
19．（本题8分）
解：（1）方法一：列表得
A
B
C
D
A
（A，B）
（A，C）
（A，D）
B
（B，A）
（B，C）
（B，D）
C
（C，A）
（C，B）
（C，D）
D
（D，A）
（D，B）
（D，C）
方法二：画树状图
（2）获奖励的概率：
．
20．（本题8分）
（1）
（2）
，
，
．
21．（本题10分）
解：（1）
是
的切线，
，
，
．
（2）
，
，
．
（3）
，
，
，
，
，
．
22．（本题12分）
解：（1）
；40；
（2）人均进球数
．
（3）设参加训练前的人均进球数为
个，由题意得：
，解得：
．
答：参加训练前的人均进球数为4个．
23．（本题12分）
（1）
（2）由题意得：
，
，
，
（m）．
（3）
，
，
设
长为
，则
，解得：
（m），即
（m）．
同理
，解得
（m），
．
24．（本题14分）
解：（1）直线的解析式为：
．
（2）方法一，
，
，
，
，
，
是等边三角形，
，
，
．
方法二，如图1，过
分别作
轴于
，
轴于
，
可求得
，
，
，
当点
与点
重合时，
，
．
，
．
（3）①当
时，见图2．
设
交
于点
，
重叠部分为直角梯形
，
作
于．
，
，
，
，
，
，
，
，
．
随
的增大而增大，
当
时，
．
②当
时，见图3．
设
交于点
，
交
于点
，交于点
，
重叠部分为五边形
．
方法一，作于，
，
，
，
．
方法二，由题意可得
，
，
，
，
再计算
，
．
，当
时，有最大值，
．
③当
时，
，即
与
重合，
设交于点，
交于点，重叠部
分为等腰梯形
，见图4．
，
综上所述：当时，
；
当时，
；
当时，
．
，
的最大值是
．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com