
题目列表(包括答案和解析)
(本题满分12分,每小题满分各4分)已知平面直角坐标系xOy(如图1),一次函数![]() 的图 像与y轴交于点A,点M在正比例函数
的图 像与y轴交于点A,点M在正比例函数![]() 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
(1)求线段AM的长;
(2)求这个二次函数的解析式;
(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图像上,点D在一次函数![]() 的图像上,且四边形ABCD是菱形,求点C的坐标.
的图像上,且四边形ABCD是菱形,求点C的坐标.
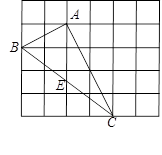
(本题满分8分)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD =BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为 ;
(3)△ACD为 三角形,四边形ABCD的面积为 ;
(4)若E为BC中点,则tan∠CAE的值是 .
(本题满分12分,每小题满分各4分)已知平面直角坐标系xOy(如图1),一次函数![]() 的图 像与y轴交于点A,点M在正比例函数
的图 像与y轴交于点A,点M在正比例函数![]() 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
(1)求线段AM的长;
(2)求这个二次函数的解析式;
(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图像上,点D在一次函数![]() 的图像上,且四边形ABCD是菱形,求点C的坐标.
的图像上,且四边形ABCD是菱形,求点C的坐标.
(本题满分13分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.

⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为![]() 时,求正方形的边长.
时,求正方形的边长.

 ,求证四边形DEBF是菱形.
,求证四边形DEBF是菱形.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com