
题目列表(包括答案和解析)
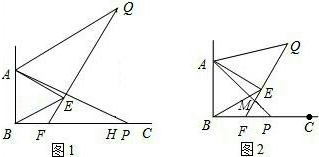
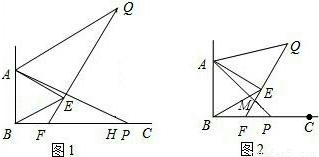
如图①,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连结AP,将AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F。
(1)如图②,当BP=BA时,∠EBF= ,猜想∠QFC= ;(2分)
(2)如图①,当点P为射线BC上任意一点时,求证∠QFC=60°;(4分)
 (3)已知线段AB=
(3)已知线段AB=![]() ,设BP=
,设BP=![]() ,点Q到射线BC的距离为
,点Q到射线BC的距离为![]() ,求
,求![]() 关于
关于![]() 的函数关系式。(4分)
的函数关系式。(4分)
 |


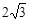 ,设BP=
,设BP=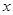 ,点Q到射线BC的距离为y,求y关于
,点Q到射线BC的距离为y,求y关于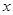 的函数关系式.
的函数关系式.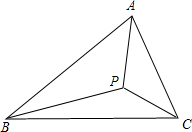
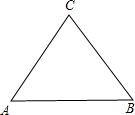
 .四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.
.四边形CDPE是正方形,CD在AC上,CE在BC上,P是△ABC的费马点.求:P点到AB的距离.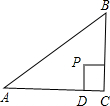
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com