．（本题满分12分）如图，三棱柱ABC—A₁B₁C₁中，AA₁⊥面ABC，BC⊥AC，BC=AC=2，AA₁=3，D为AC的中点.
（1）求证：AB₁// 面BDC₁；
（2）求二面角C₁—BD—C的余弦值；
（3）在侧棱AA­₁上是否存在点P，使得CP⊥面BDC₁？并证明你的结论.

查看答案和解析>>

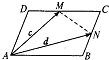（1）如图，平行四边形ABCD中，M、N分别为DC、BC的中点，已知

AM

=

c

、

AN

=

d

，试用

c

、

d

表示

AB

和

AD

．
（2）在△ABC中，若

AB

=

a

，

AC

=

b

若P，Q，S为线段BC的四等分点，试证：

AP

+

AQ

+

AS

=

3

2

(

a

+

b

)；

查看答案和解析>>

（1）已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′如图所示，其中A′D′=2，B′C′=4，A′B′=1，求直角梯形以BC为旋转轴旋转一周形成的几何体的表面积．
（2）定线段AB所在的直线与定平面α相交，P为直线AB外的一点，且P不在α内，若直线AP、BP与α分别交于C、D点，求证：不论P在什么位置，直线CD必过一定点．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

　　1．D　2．C　3．D　4．（理）D　（文）A　5．C　6．B　7．C　8．（理）C　（文）A　9．（理）B　（文）D　10．A　11．C　12．D

　　13．-2　14．6∶2∶　15．（文）7　（理）a≥3　16．（文）a≥3（理）1

　　17．解析：（1）．

　　解不等式．

　　得

　　∴　f（x）的单调增区间为，．

　　（2）∵　，]，　∴　．

　　∴　当即时，．

　　∵　3＋a＝4，∴　a＝1，此时．

　　18．解析：由已知得，，．

　　∴　．

　　欲使夹角为钝角，需．

　　得　．

　　设．

　　∴　^，∴　．

　　∴　，此时．

　　即时，向量与的夹角为p ．

　　∴　夹角为钝角时，t的取值范围是（-7，）（，）．

　　19．解析：（甲）取AD的中点G，连结VG，CG．

　　（1）∵　△ADV为正三角形，∴　VG⊥AD．

　　又平面VAD⊥平面ABCD．AD为交线，

　　∴　VG⊥平面ABCD，则∠VCG为CV与平面ABCD所成的角．

　　设AD＝a，则，．

　　在Rt△GDC中，

　　．

　　在Rt△VGC中，．

　　∴　．

　　即VC与平面ABCD成30°．

　　（2）连结GF，则．

　　而　．

　　在△GFC中，．　∴　GF⊥FC．

　　连结VF，由VG⊥平面ABCD知VF⊥FC，则∠VFG即为二面角V-FC-D的平面角．

　　在Rt△VFG中，．

　　∴　∠VFG＝45°．　二面角V-FC-B的度数为135°．

　　（3）设B到平面VFC的距离为h，当V到平面ABCD的距离是3时，即VG＝3．

　　此时，，，．

　　∴　，

　　　　．

　　∵　，

　　∴　．

　　∴　．

　　∴　　即B到面VCF的距离为．

　　（乙）以D为原点，DA、DC、所在的直线分别为x、y、z轴，建立空间直角坐标系，设正方体棱长为a，则D（0，0，0），A（a，0，0），B（a，a，0），（0，0，a），E（a，a，），F（a，，0），G（，a，0）．

　　（1），，-a），，0，，

　　∵　，

　　∴　．

　　（2），a，），

　　∴　．

　　∴　．

　　∵　，∴　平面AEG．

　　（3）由，a，），＝（a，a，），

　　∴　，．

　　20．解析：依题意，公寓2002年底建成，2003年开始使用．

　　（1）设公寓投入使用后n年可偿还全部贷款，则公寓每年收费总额为1000×80（元）＝800000（元）＝80万元，扣除18万元，可偿还贷款62万元．

　　依题意有　…．

　　化简得．

　　∴　．

　　两边取对数整理得．∴　取n＝12（年）．

　　∴　到2014年底可全部还清贷款．

　　（2）设每生和每年的最低收费标准为x元，因到2010年底公寓共使用了8年，

　　依题意有…．

　　化简得．

　　∴　（元）

　　故每生每年的最低收费标准为992元．

　　21．解析：（1），

　　而　，

　　∴　．

　　∴　{}是首项为，公差为1的等差数列．

　　（2）依题意有，而，

　　∴　．

　　对于函数，在x＞3.5时，y＞0，，在（3.5，）上为减函数．

　　故当n＝4时，取最大值3

　　而函数在x＜3.5时，y＜0，，在（，3.5）上也为减函数．

　　故当n＝3时，取最小值，＝-1．

　　（3），，

　　∴　．

　　22．解析：（1）双曲线C的右准线l的方程为：x＝，两条渐近线方程为：．

　　∴　两交点坐标为　，、，．

　　∵　△PFQ为等边三角形，则有（如图）．

　　∴　，即．

　　解得　，c＝2a．∴　．

　　（2）由（1）得双曲线C的方程为把．

　　把代入得．

　　依题意　　∴　，且．

　　∴　双曲线C被直线y＝ax＋b截得的弦长为

　　∵　．

　　∴　．

　　整理得　．

　　∴　或．

　　∴　双曲线C的方程为：或．

　　（文）（1）设B点的坐标为（0，），则C点坐标为（0，＋2）（-3≤≤1），

　　则BC边的垂直平分线为y＝＋1　　　　　　　　　　　　　　　　　 ①

　　　　　　　　　　　　　 　　　　　　　　　　　　 ②

　　由①②消去，得．

　　∵　，∴　．

　　故所求的△ABC外心的轨迹方程为：．

　　（2）将代入得．

　　由及，得．

　　所以方程①在区间，2有两个实根．

　　设，则方程③在，2上有两个不等实根的充要条件是：

　　之得．

　　∵　

　　∴　由弦长公式，得

　　又原点到直线l的距离为，

　　∴　

　　∵　，∴　．

　　∴　当，即时，．