（2011广西崇左，22，10分）（本小题满分10分）矩形、菱形、正方形都是平行四边形，但它们都是有特殊条件的平行四边形，正方形不仅是特殊的矩形，也是特殊的菱形.因此，我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题：

（1）将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.

（2）要证明一个四边形是正方形，可先证明四边形是矩形，再证明这个矩形的_______相等；或者先证明四边形是菱形，在证明这个菱形有一个角是________ .

（3）某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a²，对此结论，你认为是否正确？若正确，请说明理由；若不正确，请举出一个反例说明.

 

（本题满分10分）
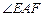（1）如图①，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高AG与正方形的边长相等，求的度数．
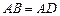（2）如图②，在Rt△ABD中，，，点M，N是BD边上的任意两点，且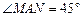，将△ABM绕点A逆时针旋转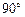至△ADH位置，连接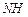，试判断MN，ND，DH之间的数量关系，并说明理由．
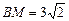（3）在图①中，连接BD分别交AE，AF于点M，N，若，，，求AG，MN的长．
        

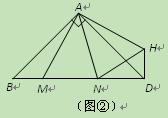
（本小题满分10分）

如图1，正方形ABCD和正方形QMNP，∠M =∠B，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．

⑴求证：ME = MF．

⑵如图2，若将原题中的“正方形”改为“菱形”，其他条件不变，探索线段ME与线段MF的关系，并加以证明．

⑶如图3，若将原题中的“正方形”改为“矩形”，且AB = mBC，其他条件不变，探索线段ME与线段MF的关系，并说明理由．

⑷根据前面的探索和图4，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题；若不能，请说明理由．

 

（本题满分10分）在边长为1的正方形网格中，有形如帆船的图案①和半径为2的⊙P．

 

 

 

 

 

 

 

 

 

 

 

1.⑴将图案①进行平移，使A点平移到点E，画出平移后的图案；

2.⑵以点M为位似中心，在网格中将图案①放大2倍，画出放大后的图案，并在放大后的图案中标出线段AB的对应线段CD；

3.⑶在⑵所画的图案中，线段CD被⊙P所截得的弦长为    ▲    （结果保留根号）．