
题目列表(包括答案和解析)
 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
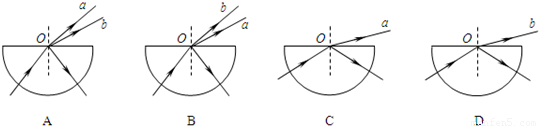
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.| V | S |
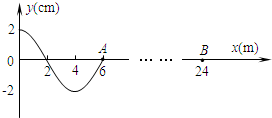
 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.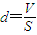

选做题:本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答。
若三题都做,则按A、B两题评分。
A.(选修模块3—3)
12下列说法正确的是 。
A.布朗运动不是液体分子的运动,但它可以说明分子在永不停息地做无规则运动
B.液体的内部分子间比液体表面层的分子间有更大的分子势能
C.分了了间距离增大时,分子间的引力和斥力都减小,它们的合力也减小
D.液晶既有液体的流动性。又具有单晶体的各向异性
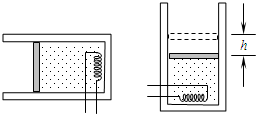
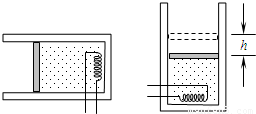
(2)如图所示,气缸与活塞封闭了一定质量的理想气体。气缸和活塞间无摩擦,且均可与外界进行热交换,若外界是环境的温度缓慢升高,则封闭气体的体积将 (增大、减小、不变),同时 (吸热、放热、既不吸热也不放热)

(3)目前专家们正在研究二拉化碳的深海处理技术。实验发现,在水深300m处,二氧化碳将变成凝胶状态。当水深超过2500m时,二氧化碳会浓缩成近似固体的硬胶体,可看成分子间是紧密排列的。已知二氧化碳的摩尔质量为M,阿伏加德罗常数为N,每个二氧化碳分子体积为V0,设在某状态下二氧化碳气体的密谋为ρ,则在该状态下为V的二氧化碳气体变成固体体积为多少?
B.(选修模块3—4)
(1)下列说法中正确的是
A.水面上的油膜在阳光照射下会呈现彩色,这是由于光的干涉造成的色散现象
B.声波与无线电波一样,都是机械振动在介质中的传播
C.用激光读取光盘上记录的信息是利用激光平行度好的特点
D.当观察者向静止的声源运动时,接收到的声音频率低于声源发出的频率
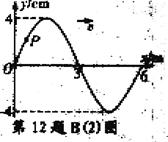
(2)一简谐横波沿x轴正方向传播,在t=0时刻的波形如图所示。已知介质中质点P的振动周期为2s,则该波传播速度为 m/s,此时P点振动方向为 (y轴正方向、y轴负方向)
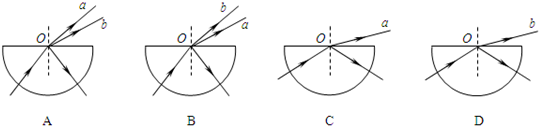
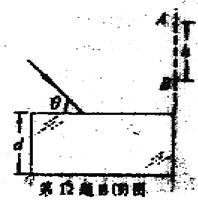
(3)如图所示,真空中平行玻璃砖折射率为![]() ,下表面镀有反射膜,一束单色光与界面成
,下表面镀有反射膜,一束单色光与界面成![]() 角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,相距h=2.0m,求玻璃砖的厚度d。
角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,相距h=2.0m,求玻璃砖的厚度d。
C.(选修模块3—5)
(1)下列关于的代物理知识说法中正确的是 。
A.将放射性元素掺杂到其它稳定元素中,并降低其温度,它的半衰期将发生改变
B.α粒子散射实验中少数α粒子发生较大的偏转是卢瑟福猜想原子核式结构模型的主要依据
C.天然放射现象的发明说明了原子核有复杂的结构
D.用质子流工作的显微镜比用相同速度的电子流工作的显微镜分辨率低
(2)氢原子的能级如图所示,有一群处于n=4能级的氢原了了,这群氢原子最多能发出 种谱线,发出的光子照射某金属能产生光电效应现象,则该金属逸出不应超过 eV。

(3)近年来,国际热核变实验堆计划取得了重大进展,它利用的核反应方程是
![]() 若
若![]() 迎面碰撞,初速度大小分别为
迎面碰撞,初速度大小分别为![]() 质量分别为
质量分别为![]() ,反应后
,反应后![]() 的速度大小为v3,方向与
的速度大小为v3,方向与![]() 的运动方向相同,求中子
的运动方向相同,求中子![]() 的速度(选取m1的运动方向为正方向,不计释放的光子的动量,不考虑相对论效率)。
的速度(选取m1的运动方向为正方向,不计释放的光子的动量,不考虑相对论效率)。
第六部分 振动和波
第一讲 基本知识介绍
《振动和波》的竞赛考纲和高考要求有很大的不同,必须做一些相对详细的补充。
一、简谐运动
1、简谐运动定义:![]() = -k
= -k![]() ①
①
凡是所受合力和位移满足①式的质点,均可称之为谐振子,如弹簧振子、小角度单摆等。
谐振子的加速度:![]() = -
= -![]()
![]()
2、简谐运动的方程
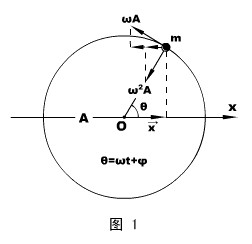
回避高等数学工具,我们可以将简谐运动看成匀速圆周运动在某一条直线上的投影运动(以下均看在x方向的投影),圆周运动的半径即为简谐运动的振幅A 。
依据:![]() x = -mω2Acosθ= -mω2
x = -mω2Acosθ= -mω2![]()
对于一个给定的匀速圆周运动,m、ω是恒定不变的,可以令:
mω2 = k
这样,以上两式就符合了简谐运动的定义式①。所以,x方向的位移、速度、加速度就是简谐运动的相关规律。从图1不难得出——
位移方程:![]() = Acos(ωt + φ) ②
= Acos(ωt + φ) ②
速度方程:![]() = -ωAsin(ωt +φ) ③
= -ωAsin(ωt +φ) ③
加速度方程:![]() = -ω2A cos(ωt +φ) ④
= -ω2A cos(ωt +φ) ④
相关名词:(ωt +φ)称相位,φ称初相。
运动学参量的相互关系:![]() = -ω2
= -ω2![]()
A = ![]()
tgφ= -![]()
3、简谐运动的合成
a、同方向、同频率振动合成。两个振动x1 = A1cos(ωt +φ1)和x2 = A2cos(ωt +φ2) 合成,可令合振动x = Acos(ωt +φ) ,由于x = x1 + x2 ,解得
A = ![]() ,φ= arctg
,φ= arctg ![]()
显然,当φ2-φ1 = 2kπ时(k = 0,±1,±2,…),合振幅A最大,当φ2-φ1 = (2k + 1)π时(k = 0,±1,±2,…),合振幅最小。
b、方向垂直、同频率振动合成。当质点同时参与两个垂直的振动x = A1cos(ωt + φ1)和y = A2cos(ωt + φ2)时,这两个振动方程事实上已经构成了质点在二维空间运动的轨迹参数方程,消去参数t后,得一般形式的轨迹方程为
![]() +
+![]() -2
-2![]() cos(φ2-φ1) = sin2(φ2-φ1)
cos(φ2-φ1) = sin2(φ2-φ1)
显然,当φ2-φ1 = 2kπ时(k = 0,±1,±2,…),有y = ![]() x ,轨迹为直线,合运动仍为简谐运动;
x ,轨迹为直线,合运动仍为简谐运动;
当φ2-φ1 = (2k + 1)π时(k = 0,±1,±2,…),有![]() +
+![]() = 1 ,轨迹为椭圆,合运动不再是简谐运动;
= 1 ,轨迹为椭圆,合运动不再是简谐运动;
当φ2-φ1取其它值,轨迹将更为复杂,称“李萨如图形”,不是简谐运动。
c、同方向、同振幅、频率相近的振动合成。令x1 = Acos(ω1t + φ)和x2 = Acos(ω2t + φ) ,由于合运动x = x1 + x2 ,得:x =(2Acos![]() t)cos(
t)cos(![]() t +φ)。合运动是振动,但不是简谐运动,称为角频率为
t +φ)。合运动是振动,但不是简谐运动,称为角频率为![]() 的“拍”现象。
的“拍”现象。
4、简谐运动的周期
由②式得:ω= ![]() ,而圆周运动的角速度和简谐运动的角频率是一致的,所以
,而圆周运动的角速度和简谐运动的角频率是一致的,所以
T = 2π![]() ⑤
⑤
5、简谐运动的能量
一个做简谐运动的振子的能量由动能和势能构成,即
![]() =
= ![]() mv2 +
mv2 + ![]() kx2 =
kx2 = ![]() kA2
kA2
注意:振子的势能是由(回复力系数)k和(相对平衡位置位移)x决定的一个抽象的概念,而不是具体地指重力势能或弹性势能。当我们计量了振子的抽象势能后,其它的具体势能不能再做重复计量。
6、阻尼振动、受迫振动和共振
和高考要求基本相同。
二、机械波
1、波的产生和传播
产生的过程和条件;传播的性质,相关参量(决定参量的物理因素)
2、机械波的描述
a、波动图象。和振动图象的联系
b、波动方程
如果一列简谐波沿x方向传播,振源的振动方程为y = Acos(ωt + φ),波的传播速度为v ,那么在离振源x处一个振动质点的振动方程便是
y = Acos〔ωt + φ - ![]() ·2π〕= Acos〔ω(t -
·2π〕= Acos〔ω(t - ![]() )+ φ〕
)+ φ〕
这个方程展示的是一个复变函数。对任意一个时刻t ,都有一个y(x)的正弦函数,在x-y坐标下可以描绘出一个瞬时波形。所以,称y = Acos〔ω(t - ![]() )+ φ〕为波动方程。
)+ φ〕为波动方程。
3、波的干涉
a、波的叠加。几列波在同一介质种传播时,能独立的维持它们的各自形态传播,在相遇的区域则遵从矢量叠加(包括位移、速度和加速度的叠加)。
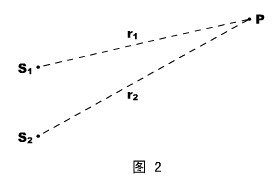
b、波的干涉。两列波频率相同、相位差恒定时,在同一介质中的叠加将形成一种特殊形态:振动加强的区域和振动削弱的区域稳定分布且彼此隔开。
我们可以用波程差的方法来讨论干涉的定量规律。如图2所示,我们用S1和S2表示两个波源,P表示空间任意一点。
当振源的振动方向相同时,令振源S1的振动方程为y1 = A1cosωt ,振源S1的振动方程为y2 = A2cosωt ,则在空间P点(距S1为r1 ,距S2为r2),两振源引起的分振动分别是
y1′= A1cos〔ω(t ? ![]() )〕
)〕
y2′= A2cos〔ω(t ? ![]() )〕
)〕
P点便出现两个频率相同、初相不同的振动叠加问题(φ1 = ![]() ,φ2 =
,φ2 = ![]() ),且初相差Δφ=
),且初相差Δφ= ![]() (r2 – r1)。根据前面已经做过的讨论,有
(r2 – r1)。根据前面已经做过的讨论,有
r2 ? r1 = kλ时(k = 0,±1,±2,…),P点振动加强,振幅为A1 + A2 ;
r2 ? r1 =(2k ? 1)![]() 时(k = 0,±1,±2,…),P点振动削弱,振幅为│A1-A2│。
时(k = 0,±1,±2,…),P点振动削弱,振幅为│A1-A2│。
4、波的反射、折射和衍射
知识点和高考要求相同。
5、多普勒效应
当波源或者接受者相对与波的传播介质运动时,接收者会发现波的频率发生变化。多普勒效应的定量讨论可以分为以下三种情况(在讨论中注意:波源的发波频率f和波相对介质的传播速度v是恒定不变的)——
a、只有接收者相对介质运动(如图3所示)
设接收者以速度v1正对静止的波源运动。
如果接收者静止在A点,他单位时间接收的波的个数为f ,
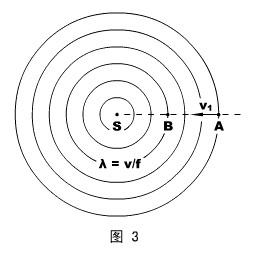
当他迎着波源运动时,设其在单位时间到达B点,则![]() = v1 ,、
= v1 ,、
在从A运动到B的过程中,接收者事实上“提前”多接收到了n个波
n = ![]() =
= ![]() =
= ![]()
显然,在单位时间内,接收者接收到的总的波的数目为:f + n = ![]() f ,这就是接收者发现的频率f1 。即
f ,这就是接收者发现的频率f1 。即
f1 = ![]() f
f
显然,如果v1背离波源运动,只要将上式中的v1代入负值即可。如果v1的方向不是正对S ,只要将v1出正对的分量即可。
b、只有波源相对介质运动(如图4所示)
设波源以速度v2正对静止的接收者运动。
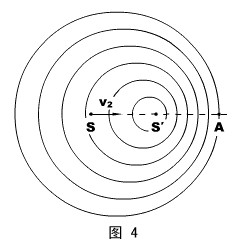
如果波源S不动,在单位时间内,接收者在A点应接收f个波,故S到A的距离:![]() = fλ
= fλ
在单位时间内,S运动至S′,即![]() = v2 。由于波源的运动,事实造成了S到A的f个波被压缩在了S′到A的空间里,波长将变短,新的波长
= v2 。由于波源的运动,事实造成了S到A的f个波被压缩在了S′到A的空间里,波长将变短,新的波长
λ′= ![]() =
= ![]() =
= ![]() =
= ![]()
而每个波在介质中的传播速度仍为v ,故“被压缩”的波(A接收到的波)的频率变为
f2 = ![]() =
= ![]() f
f
当v2背离接收者,或有一定夹角的讨论,类似a情形。
c、当接收者和波源均相对传播介质运动
当接收者正对波源以速度v1(相对介质速度)运动,波源也正对接收者以速度v2(相对介质速度)运动,我们的讨论可以在b情形的过程上延续…
![]() f3 =
f3 = ![]() f2 =
f2 = ![]() f
f
关于速度方向改变的问题,讨论类似a情形。
6、声波
a、乐音和噪音
b、声音的三要素:音调、响度和音品
c、声音的共鸣
第二讲 重要模型与专题
一、简谐运动的证明与周期计算
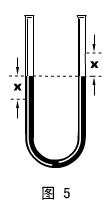
物理情形:如图5所示,将一粗细均匀、两边开口的U型管固定,其中装有一定量的水银,汞柱总长为L 。当水银受到一个初始的扰动后,开始在管中振动。忽略管壁对汞的阻力,试证明汞柱做简谐运动,并求其周期。
模型分析:对简谐运动的证明,只要以汞柱为对象,看它的回复力与位移关系是否满足定义式①,值得注意的是,回复力![]() 系指振动方向上的合力(而非整体合力)。当简谐运动被证明后,回复力系数k就有了,求周期就是顺理成章的事。
系指振动方向上的合力(而非整体合力)。当简谐运动被证明后,回复力系数k就有了,求周期就是顺理成章的事。
本题中,可设汞柱两端偏离平衡位置的瞬时位移为x 、水银密度为ρ、U型管横截面积为S ,则次瞬时的回复力
ΣF = ρg2xS = ![]() x
x
由于L、m为固定值,可令:![]() = k ,而且ΣF与x的方向相反,故汞柱做简谐运动。
= k ,而且ΣF与x的方向相反,故汞柱做简谐运动。
周期T = 2π![]() = 2π
= 2π![]()
答:汞柱的周期为2π![]() 。
。

学生活动:如图6所示,两个相同的柱形滚轮平行、登高、水平放置,绕各自的轴线等角速、反方向地转动,在滚轮上覆盖一块均质的木板。已知两滚轮轴线的距离为L 、滚轮与木板之间的动摩擦因素为μ、木板的质量为m ,且木板放置时,重心不在两滚轮的正中央。试证明木板做简谐运动,并求木板运动的周期。
思路提示:找平衡位置(木板重心在两滚轮中央处)→ú力矩平衡和Σ?F6= 0结合求两处弹力→ú求摩擦力合力…
答案:木板运动周期为2π![]() 。
。
巩固应用:如图7所示,三根长度均为L = 2.00m地质量均匀直杆,构成一正三角形框架ABC,C点悬挂在一光滑水平轴上,整个框架可绕转轴转动。杆AB是一导轨,一电动松鼠可在导轨上运动。现观察到松鼠正在导轨上运动,而框架却静止不动,试讨论松鼠的运动是一种什么样的运动。
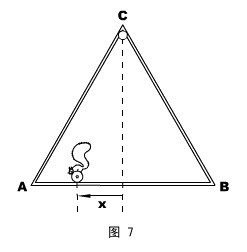
解说:由于框架静止不动,松鼠在竖直方向必平衡,即:松鼠所受框架支持力等于松鼠重力。设松鼠的质量为m ,即:
N = mg ①
再回到框架,其静止平衡必满足框架所受合力矩为零。以C点为转轴,形成力矩的只有松鼠的压力N、和松鼠可能加速的静摩擦力f ,它们合力矩为零,即:
MN = Mf
现考查松鼠在框架上的某个一般位置(如图7,设它在导轨方向上距C点为x),上式即成:
N·x = f·Lsin60° ②
解①②两式可得:f = ![]() x ,且f的方向水平向左。
x ,且f的方向水平向左。
根据牛顿第三定律,这个力就是松鼠在导轨方向上的合力。如果我们以C在导轨上的投影点为参考点,x就是松鼠的瞬时位移。再考虑到合力与位移的方向因素,松鼠的合力与位移满足关系——
![]() = -k
= -k![]()
其中k = ![]() ,对于这个系统而言,k是固定不变的。
,对于这个系统而言,k是固定不变的。
显然这就是简谐运动的定义式。
答案:松鼠做简谐运动。
评说:这是第十三届物理奥赛预赛试题,问法比较模糊。如果理解为定性求解,以上答案已经足够。但考虑到原题中还是有定量的条件,所以做进一步的定量运算也是有必要的。譬如,我们可以求出松鼠的运动周期为:T = 2π![]() = 2π
= 2π![]() = 2.64s 。
= 2.64s 。
二、典型的简谐运动
1、弹簧振子
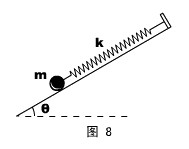
物理情形:如图8所示,用弹性系数为k的轻质弹簧连着一个质量为m的小球,置于倾角为θ
第十部分 磁场
第一讲 基本知识介绍
《磁场》部分在奥赛考刚中的考点很少,和高考要求的区别不是很大,只是在两处有深化:a、电流的磁场引进定量计算;b、对带电粒子在复合场中的运动进行了更深入的分析。
一、磁场与安培力
1、磁场
a、永磁体、电流磁场→磁现象的电本质
b、磁感强度、磁通量
c、稳恒电流的磁场
*毕奥-萨伐尔定律(Biot-Savart law):对于电流强度为I 、长度为dI的导体元段,在距离为r的点激发的“元磁感应强度”为dB 。矢量式d![]() = k
= k![]() ,(d
,(d![]() 表示导体元段的方向沿电流的方向、
表示导体元段的方向沿电流的方向、![]() 为导体元段到考查点的方向矢量);或用大小关系式dB = k
为导体元段到考查点的方向矢量);或用大小关系式dB = k![]() 结合安培定则寻求方向亦可。其中 k = 1.0×10?7N/A2 。应用毕萨定律再结合矢量叠加原理,可以求解任何形状导线在任何位置激发的磁感强度。
结合安培定则寻求方向亦可。其中 k = 1.0×10?7N/A2 。应用毕萨定律再结合矢量叠加原理,可以求解任何形状导线在任何位置激发的磁感强度。
毕萨定律应用在“无限长”直导线的结论:B = 2k![]() ;
;
*毕萨定律应用在环形电流垂直中心轴线上的结论:B = 2πkI![]() ;
;
*毕萨定律应用在“无限长”螺线管内部的结论:B = 2πknI 。其中n为单位长度螺线管的匝数。
2、安培力
a、对直导体,矢量式为 ![]() = I
= I![]() ;或表达为大小关系式 F = BILsinθ再结合“左手定则”解决方向问题(θ为B与L的夹角)。
;或表达为大小关系式 F = BILsinθ再结合“左手定则”解决方向问题(θ为B与L的夹角)。
b、弯曲导体的安培力
⑴整体合力
折线导体所受安培力的合力等于连接始末端连线导体(电流不变)的的安培力。
证明:参照图9-1,令MN段导体的安培力F1与NO段导体的安培力F2的合力为F,则F的大小为
F = ![]()
= BI![]()
= BI![]()
关于F的方向,由于ΔFF2P∽ΔMNO,可以证明图9-1中的两个灰色三角形相似,这也就证明了F是垂直MO的,再由于ΔPMO是等腰三角形(这个证明很容易),故F在MO上的垂足就是MO的中点了。
证毕。
由于连续弯曲的导体可以看成是无穷多元段直线导体的折合,所以,关于折线导体整体合力的结论也适用于弯曲导体。(说明:这个结论只适用于匀强磁场。)
⑵导体的内张力
弯曲导体在平衡或加速的情形下,均会出现内张力,具体分析时,可将导体在被考查点切断,再将被切断的某一部分隔离,列平衡方程或动力学方程求解。
c、匀强磁场对线圈的转矩
如图9-2所示,当一个矩形线圈(线圈面积为S、通以恒定电流I)放入匀强磁场中,且磁场B的方向平行线圈平面时,线圈受安培力将转动(并自动选择垂直B的中心轴OO′,因为质心无加速度),此瞬时的力矩为
M = BIS
几种情形的讨论——
⑴增加匝数至N ,则 M = NBIS ;
⑵转轴平移,结论不变(证明从略);
⑶线圈形状改变,结论不变(证明从略);
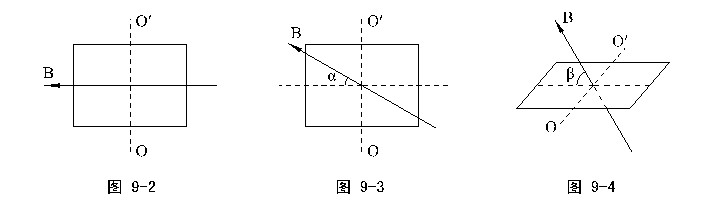
*⑷磁场平行线圈平面相对原磁场方向旋转α角,则M = BIScosα ,如图9-3;
证明:当α = 90°时,显然M = 0 ,而磁场是可以分解的,只有垂直转轴的的分量Bcosα才能产生力矩…
⑸磁场B垂直OO′轴相对线圈平面旋转β角,则M = BIScosβ ,如图9-4。
证明:当β = 90°时,显然M = 0 ,而磁场是可以分解的,只有平行线圈平面的的分量Bcosβ才能产生力矩…
说明:在默认的情况下,讨论线圈的转矩时,认为线圈的转轴垂直磁场。如果没有人为设定,而是让安培力自行选定转轴,这时的力矩称为力偶矩。
二、洛仑兹力
1、概念与规律
a、![]() = q
= q![]() ,或展开为f = qvBsinθ再结合左、右手定则确定方向(其中θ为
,或展开为f = qvBsinθ再结合左、右手定则确定方向(其中θ为![]() 与
与![]() 的夹角)。安培力是大量带电粒子所受洛仑兹力的宏观体现。
的夹角)。安培力是大量带电粒子所受洛仑兹力的宏观体现。
b、能量性质
由于![]() 总垂直
总垂直![]() 与
与![]() 确定的平面,故
确定的平面,故![]() 总垂直
总垂直![]() ,只能起到改变速度方向的作用。结论:洛仑兹力可对带电粒子形成冲量,却不可能做功。或:洛仑兹力可使带电粒子的动量发生改变却不能使其动能发生改变。
,只能起到改变速度方向的作用。结论:洛仑兹力可对带电粒子形成冲量,却不可能做功。或:洛仑兹力可使带电粒子的动量发生改变却不能使其动能发生改变。
问题:安培力可以做功,为什么洛仑兹力不能做功?
解说:应该注意“安培力是大量带电粒子所受洛仑兹力的宏观体现”这句话的确切含义——“宏观体现”和“完全相等”是有区别的。我们可以分两种情形看这个问题:(1)导体静止时,所有粒子的洛仑兹力的合力等于安培力(这个证明从略);(2)导体运动时,粒子参与的是沿导体棒的运动v1和导体运动v2的合运动,其合速度为v ,这时的洛仑兹力f垂直v而安培力垂直导体棒,它们是不可能相等的,只能说安培力是洛仑兹力的分力f1 = qv1B的合力(见图9-5)。
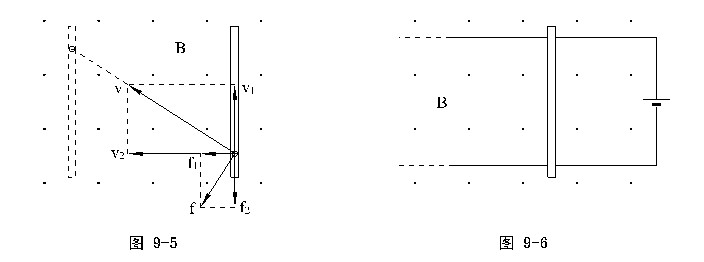
很显然,f1的合力(安培力)做正功,而f不做功(或者说f1的正功和f2的负功的代数和为零)。(事实上,由于电子定向移动速率v1在10?5m/s数量级,而v2一般都在10?2m/s数量级以上,致使f1只是f的一个极小分量。)
☆如果从能量的角度看这个问题,当导体棒放在光滑的导轨上时(参看图9-6),导体棒必获得动能,这个动能是怎么转化来的呢?
若先将导体棒卡住,回路中形成稳恒的电流,电流的功转化为回路的焦耳热。而将导体棒释放后,导体棒受安培力加速,将形成感应电动势(反电动势)。动力学分析可知,导体棒的最后稳定状态是匀速运动(感应电动势等于电源电动势,回路电流为零)。由于达到稳定速度前的回路电流是逐渐减小的,故在相同时间内发的焦耳热将比导体棒被卡住时少。所以,导体棒动能的增加是以回路焦耳热的减少为代价的。
2、仅受洛仑兹力的带电粒子运动
a、![]() ⊥
⊥![]() 时,匀速圆周运动,半径r =
时,匀速圆周运动,半径r = ![]() ,周期T =
,周期T = ![]()
b、![]() 与
与![]() 成一般夹角θ时,做等螺距螺旋运动,半径r =
成一般夹角θ时,做等螺距螺旋运动,半径r = ![]() ,螺距d =
,螺距d = ![]()
这个结论的证明一般是将![]() 分解…(过程从略)。
分解…(过程从略)。
☆但也有一个问题,如果将![]() 分解(成垂直速度分量B2和平行速度分量B1 ,如图9-7所示),粒子的运动情形似乎就不一样了——在垂直B2的平面内做圆周运动?
分解(成垂直速度分量B2和平行速度分量B1 ,如图9-7所示),粒子的运动情形似乎就不一样了——在垂直B2的平面内做圆周运动?
其实,在图9-7中,B1平行v只是一种暂时的现象,一旦受B2的洛仑兹力作用,v改变方向后就不再平行B1了。当B1施加了洛仑兹力后,粒子的“圆周运动”就无法达成了。(而在分解v的处理中,这种局面是不会出现的。)
3、磁聚焦
a、结构:见图9-8,K和G分别为阴极和控制极,A为阳极加共轴限制膜片,螺线管提供匀强磁场。
b、原理:由于控制极和共轴膜片的存在,电子进磁场的发散角极小,即速度和磁场的夹角θ极小,各粒子做螺旋运动时可以认为螺距彼此相等(半径可以不等),故所有粒子会“聚焦”在荧光屏上的P点。
4、回旋加速器
a、结构&原理(注意加速时间应忽略)
b、磁场与交变电场频率的关系
因回旋周期T和交变电场周期T′必相等,故 ![]() =
=![]()
c、最大速度 vmax = ![]() = 2πRf
= 2πRf
5、质谱仪
速度选择器&粒子圆周运动,和高考要求相同。
第二讲 典型例题解析
一、磁场与安培力的计算
【例题1】两根无限长的平行直导线a、b相距40cm,通过电流的大小都是3.0A,方向相反。试求位于两根导线之间且在两导线所在平面内的、与a导线相距10cm的P点的磁感强度。
【解说】这是一个关于毕萨定律的简单应用。解题过程从略。
【答案】大小为8.0×10?6T ,方向在图9-9中垂直纸面向外。
【例题2】半径为R ,通有电流I的圆形线圈,放在磁感强度大小为B 、方向垂直线圈平面的匀强磁场中,求由于安培力而引起的线圈内张力。
【解说】本题有两种解法。
方法一:隔离一小段弧,对应圆心角θ ,则弧长L = θR 。因为θ →
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com