①沿直线做匀加速运动的某物体,牵引一条通过打点计时器的纸带,计时器的打点周期T=0.02s,取下纸带后,由某一计时点开始,每隔五个点剪下一段纸带,按图1那样贴在直角坐标平面上,彼此不留间隙,也不要重叠.纸带下端都要准确地与横轴重合,每一条纸带的左边准确地与纵轴平行,图的纵轴上已标出了每条纸带的长度L(单位:mm).今以横轴为时间轴,令每条纸带的宽度代表一个时间单位:0.1s,以纵轴为速度轴,纵轴上原来标的每毫米代表一个速度单位:10mm/s.
(1)在每段纸带的上边缘中点画“?”作为计数点,在新的坐标里每个计数点的纵坐标表示______.
(2)画一直线,使尽可能多的计数点落在此直线上,并使直线两侧的计数点数目大致相等,这条直线便是运动物体的______图线.
(3)求出上述直线的斜率,可知运动物体的加速度a=______m/s
2.
②在“探究加速度与力、质量的关系”的实验时:
(1)我们已经知道,物体的加速度(a)同时跟合外力(F)和质量(m)两个因素有关.要研究这三个物理量之间的定量关系的基本思路是______

(2)某同学的实验方案如图2所示,她想用砂和砂桶的重力表示小车受到的合外力,为了减少这种做法而带来的实验误差,你认为在实验中还应该采取的两项措施是:a.______;b.______.
(3)该同学利用实验中打出的纸带求加速度时,处理方案有两种:
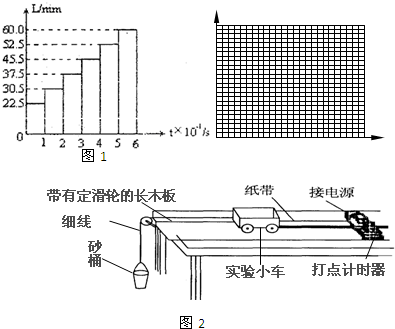
A、利用公式a=
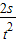
计算;B、根据a=
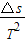
利用逐差法计算.
两种方案中,你认为选择方案______比较合理.
(4)下表是该同学在探究“保持m不变,a与F的关系”时记录的一组实验数据,请你根据表格中的数据在下面的坐标系中做出a-F图象;
( 小车质量:M=0.500kg,g=10m/s
2 )
次数
物理量 | 1 | 2 | 3 | 4 | 5 | 6 |
| m砂和桶(kg) | 0.010 | 0.020 | 0.030 | 0.040 | 0.050 | 0.060 |
| a(m/s2) | 0.196 | 0.390 | 0.718 | 0.784 | 0.990 | 1.176 |
(5)针对该同学的实验设计、实验操作、数据采集与处理,就其中的某一环节,提出一条你有别于该同学的设计或处理方法:______.


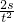 计算;B、根据a=
计算;B、根据a=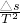 利用逐差法计算.
利用逐差法计算.
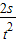 计算;B、根据a=
计算;B、根据a=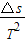 利用逐差法计算.
利用逐差法计算.