
题目列表(包括答案和解析)
解:(1)点C的坐标为![]() .
.
∵ 点A、B的坐标分别为![]() ,
,
∴ 可设过A、B、C三点的抛物线的解析式为![]() .
.
将![]() 代入抛物线的解析式,得
代入抛物线的解析式,得![]() .
.
∴ 过A、B、C三点的抛物线的解析式为![]() .
.
 (2)可得抛物线的对称轴为
(2)可得抛物线的对称轴为![]() ,顶点D的坐标为
,顶点D的坐标为
![]() ,设抛物线的对称轴与x轴的交点为G.
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为![]() .
.
设点P的坐标为![]() .
.
解法一:如图8,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ![]() ,即
,即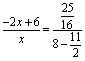 .
.
解得![]() . 经检验
. 经检验![]() 是原方程的解.
是原方程的解.
此时点P的坐标为![]() .
.
但此时![]() ,OM<GA.
,OM<GA.
∵ ![]()
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P. - - - - - - - - - - - - - - - - - - - - - 6分
解法二:如图9,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于
点N. 则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由![]() ,可得E点的坐标为
,可得E点的坐标为![]() .
.
NE=EG=![]() , ON=OE-NE=
, ON=OE-NE=![]() ,NP=DG=
,NP=DG=![]() .
.
∴ 点P的坐标为![]() .∵ x=
.∵ x=![]() 时,
时,![]() ,
,
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P .

(3)![]() 的取值范围是
的取值范围是![]() .
.
| 2 |
| x+1 |
| 3 |
| x-1 |
| 6 |
| x2-1 |
| A、方程两边分式的最简公分母是x2-1 |
| B、方程两边都乘以(x2-1),得整式方程2(x-1)+3(x+1)=6 |
| C、解这个整式方程得:x=1 |
| D、原方程的解为x=1 |
| 2 |
| x+1 |
| 3 |
| x-1 |
| 6 |
| x2-1 |
| A.方程两边分式的最简公分母是x2-1 |
| B.方程两边都乘以(x2-1),得整式方程2(x-1)+3(x+1)=6 |
| C.解这个整式方程得:x=1 |
| D.原方程的解为x=1 |
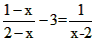 得步骤是:①方程两边都乘以最简公分母(x-2),得整式方程( );解整式方程x=( );把结果代入最简公分母,得x-2=( );所以x=( );是原方程的( );应舍去,原方程无解。
得步骤是:①方程两边都乘以最简公分母(x-2),得整式方程( );解整式方程x=( );把结果代入最简公分母,得x-2=( );所以x=( );是原方程的( );应舍去,原方程无解。 +
+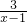 =
=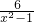 ,下列四步中,错误的一步是
,下列四步中,错误的一步是湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com